Esboce o gráfico:

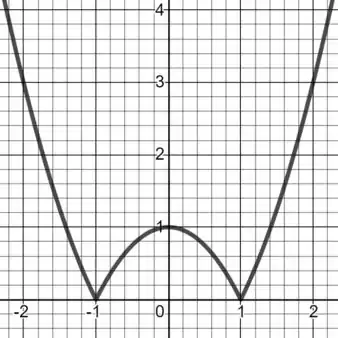
Neste caso temos uma função do segundo grau, ou seja, seu gráfico é uma parábola.

O gráfico de é uma concavidade voltada para cima e que para cada valor de temos um valor de que é o seu quadrado menos uma unidade, então basta pensar no gráfico de e “descer” a parábola em uma unidade no eixo , mas por estár dentro do módulo, todo valor negativo da parábola ficará positivo, então basta “refletir” essa parte do gráfico para cima do eixo .