Enunciado
Cálculo - Um curso de Cálculo Volume 1 - 5ª Edição - Hamilton Luiz Guidorizzi- Ed: 5º - Capítulo 6.1 - Ex. 2f
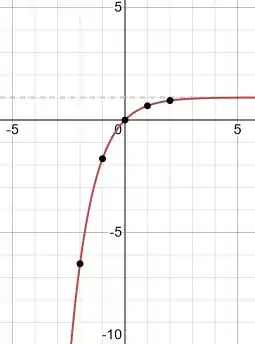
Esboce o gráfico.
Passo 1
Vamos primeiro fazer uma manipulação:
Sabemos de cara que como a função é estritamente decrescente em e como é negativa ela está no eixo invertido em relação ao eixo de , além de está somado a , deslocando o gráfico em pra cima.
Para construir o gráfico vamos admitir valores de para poder traçar:
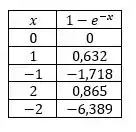
Agora é só colocar esses pontos no gráfico:
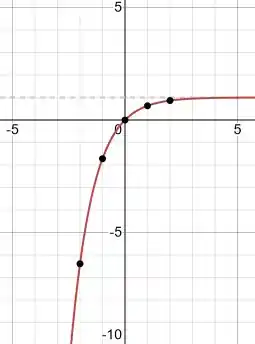
Resposta
Exercícios de Livros Relacionados
Construir o gráfico das seguintes funções exponenciais: y = a x ,s ea = 2,1 / 2 , e y = 10 1 x y = e - x 2 y = - 2 x
Construir o gráfico das seguintes funções exponenciais: y = a x ,s ea = 2,1 / 2 , e y = 10 1 x y = e - x 2 y = - 2 x
Analisar a função f x = 24 x - 3 x 2 e verificar a possibilidade de representar uma função receita total. Em caso afirmativo identifique a função demanda e responda:Qual a quantidade demandada quando
Uma indústria comercializa um certo produto e tem uma função custo total dada por C x = x 2 + 20 x + 700 , sendo x o número de unidades produzidas. A função receita total é dada por R x = 200 x . Dete
Uma caixa sem tampa, na forma de um paralelepípedo, tem um volume de 10c m 3 . O comprimento da base é o dobro da largura. O material da base custa R $2,00 por m 2 ao passo que o material das laterais