Enunciado
Cálculo - Anton - Cálculo - Vol 1- Ed: 10º - Capítulo 0.3 - Ex. 21
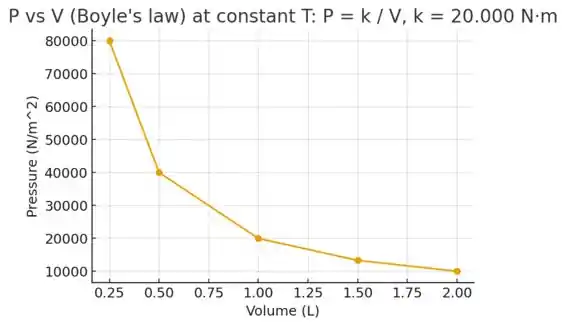
Conforme discutido nesta seção, a lei de Boyle estabelece que, a uma temperatura constante, a pressão P exercida por um gás está relacionada ao volume V pela equação PV=k.
(a) Encontre as unidades apropriadas para a constante k se a pressão (que é força por unidade de área) for em newtons por metro quadrado (n/m^2) e o volume, em metros cúbicos.
(b) Encontre k se o gás exercer uma pressão de 20000 N/m^2 quando o volume for de 1 litro (0,001 m^3)
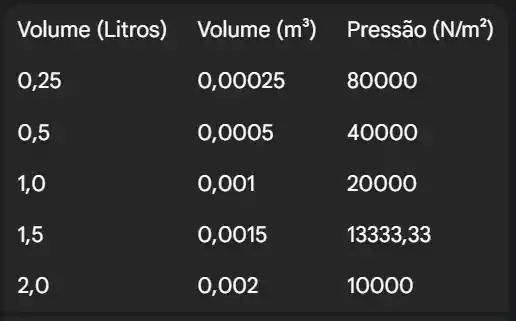
(c) Faça uma tabela que mostre as pressões para volumes de 0,25, 0,5, 1, 1,5 e 2 litros
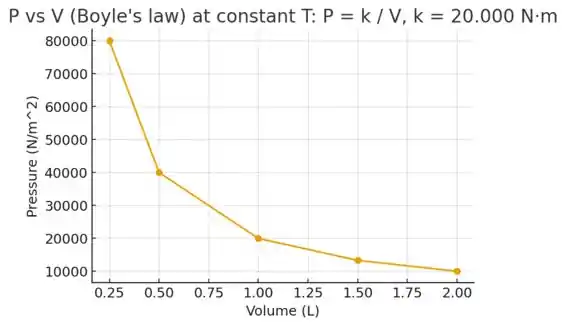
(d) Faça o gráfico de P versus V.
Passo 1
(a) Bom, para encontrar , nós usamos a fórmula dada no enunciado:
Então, a unidade para a constante será o produto das unidades de pressão e volume! Dessa forma:
Assim, podemos fazer as contas normalmente. Vamos cortar com :
Logo, a unidade de é .
Passo 2
(b) Aqui, vamos apenas usar a fórmula:
Queremos , se e . Substituindo na fórmula:
Passo 3
(c) Usando o valor de e vamos descobrir os valores das pressões variando o volume na fórmula:
Para :
Para :
Para :
Para :
Para :
Montando uma tabela com esses valores:
Passo 4
(d) Para fazer o gráfico, vamos apenas jogar os pontos da tabela que montamos no passo anterior em um gráfico e ligá-los:
Ligando os pontos:
Resposta
(a)
(b)
(c)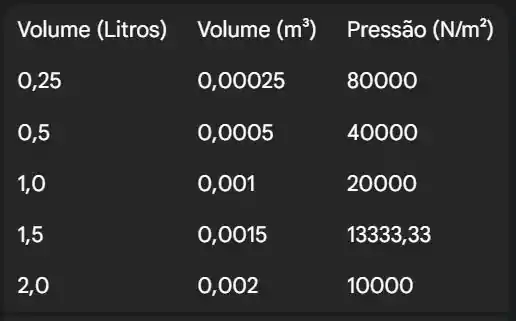 
(d) 