Enunciado
Cálculo - Cálculo Volume 2 - 5ª Edição - James Stewart- Ed: 5º - Capítulo 16.1 - Ex. 27
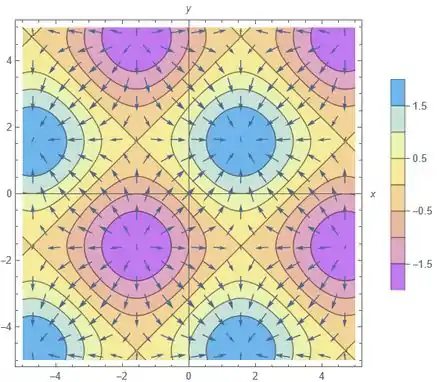
Trace o campo vetorial gradiente de e o mapa de contorno de . Explique como eles estão relacionados.
Passo 1
Falaa, povo!
Nessa questão precisamos usar um software pra desenhar o campo vetorial gradiente e o mapa de contorno de uma função:
Vamos usar o Mathematica pra fazer isso.
Lembrando que o campo gradiente nós calculamos assim:
Depois, com o desenho, vamos explicar como eles se relacionam.
Passo 2
Vamos começar calculando as derivadas parciais pra encontrar o vetor gradiente.
Primeiro derivamos em função de , considerando como constante:
E em função de , com constante:
O campo gradiente é esse aqui:
Passo 3
Bom, os comandos que vamos usar no Mathematica pra plotar isso são:
- VectorPlot para desenhar o campo vetorial
- ContourPlot para desenhar o mapa de contorno
- Show para mostrar os dois desenhos ao mesmo tempo
Então o comando todo fica assim:
Esses componentes dentro das funções servem pra deixar o nosso desenho com uma visualização melhor.
O retorno do software é esse:
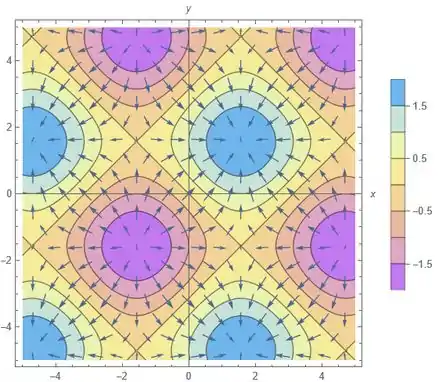
Passo 4
Agora vamos observar essa imagem pra explicar a relação entre os vetores e as curvas de nível.
Percebe que nas regiões em rosa os vetores apontam pra fora, e nas regiões azul apontam pra dentro. Se olharmos pra legenda das cores, vemos que isso quer dizer que o campo gradiente está apontando na direção do crescimento de !
Além disso, nessas regiões que parecem circulares (ou próximas de um círculo), os vetores parecem estar partindo ou apontando para o centro delas. Com relação às curvas, os vetores acabam estando sempre perpendiculares às curvas de nível!
Resposta
