O campo representa a velocidade de um volante em rotação rígida em torno do eixo z. Descrever graficamente o campo. Qual o sentido do movimento de rotação?
Passo 1
Bom galera, aqui não é nada muito complicado.
Nós temos a nossa função vetorial associa a cada ponto do plano o seu vetor posição .
Nós não temos nenhuma limitação quanto aos valores de x e y, então basta nós substituirmos alguns pontos:
Então cada ponto terá um vetor correspondente, e se fizermos muitos pontos vetores vamos chegar em algo do tipo:
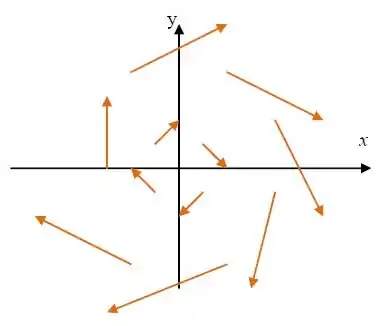
Já sabem qual o sentido? Horário, certo?
E fiiim !!