Enunciado
Cálculo - Diva Flemming - Cálculo A- Ed: 6º - Capítulo 2.17 - Ex. 50b
Determine algebricamente a função inversa. A seguir, numa mesma janela, trace o gráfico de cada função, de sua inversa e da função identidade.
b)
Passo 1
Então galera, para determinarmos a inversa de uma função devemos apenas isolar a variável independente, que no nosso caso é o . Para a nossa função, se fizermos isso, teremos:
Agora que isolamos vamos trocar de lugar as variáveis e . Fazemos isso porque estamos acostumados a ter uma função e não , logo:
Passo 2
Ok, acabamos de determinar a nossa função inversa! O que devemos fazer agora é traçar o gráfico da função, da sua inversa e da função identidade. Aqui vale ressaltar que a função identidade é uma função dos quadrantes ímpares, que é escrita da seguinte forma:
Plotando os gráficos, teremos:
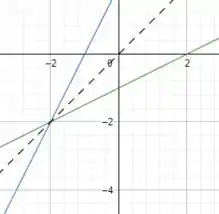
No qual a função em verde é a nossa função original, a função em azul é a função inversa e a função pontilhada é a função identidade. Está aí nosso resultado!
Resposta
