Enunciado
Cálculo - James Stewart - Vol 1- Ed: 8º - Capítulo 2.2 - Ex. 16
Esboce o gráfico de um exemplo de função que satisfaça todas as condições dadas.
Passo 1
Beleza, meu nobre.
Aqui iremos desenhar um gráfico de uma função que seja capaz de satisfazer todas as condições dadas. Essa função deve ter:
Uma observação é que a função não precisa ser necessariamente definida por apenas uma lei de formação, caso necessário podemos ter diferentes leis para diferentes intervalos.
Passo 2
Bom pessoal, vamos aos limites:
- Isto quer dizer que quando o se aproxima do eixo pela esquerda, o valor de tende a .
- Isto quer dizer que quando o se aproxima do eixo pela direita, o valor de tende a .
- Isto quer dizer que quando o se aproxima de pela esquerda, o valor de tende a .
- Isto quer dizer que quando o se aproxima de pela direita, o valor de tende a .
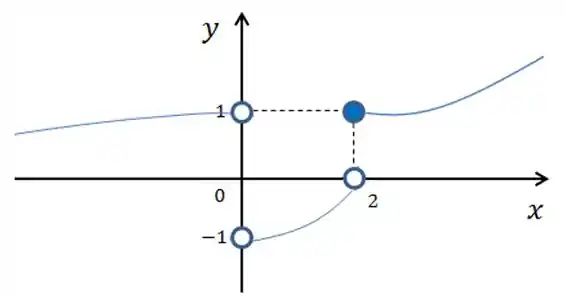
Podemos então esboçar a curva:
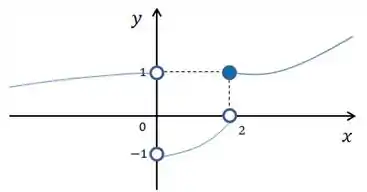
Note que as bolinhas brancas no eixo indicam a outra condição do enunciado: não estar definido. Alguma dessas bolinhas seria pintada se fosse o caso de estar definido, assim como pra tem bolinha pintada, já que o enunciado define
Resposta
Exercícios de Livros Relacionados
Ache, se existirema ) underset(x - 2^+)(lim) ⟦x⟧ ⟦ ⟧b ) underset(x - 2^-)(lim) ⟦x⟧ ⟦ ⟧c ) underset(x - 2)(lim) ⟦x⟧ ⟦ ⟧
F (x) = x - 2 sgn x Lembrando que sgn x é definido como sgn x = {[[-,1,s,e,x,,0],[0,s,e,x,=,0],[1,s,e,x,,0]]) Ache, se existirem:a ) underset(x - 0^+)(lim) F (x) b ) underset(x - 0^-)(lim) F (x) c ) u
Ache, se existirema ) underset(x - 4^+)(lim) ⟦x - 3⟧ ⟦ ⟧b ) underset(x - 4^-)(lim) ⟦x - 3⟧ ⟦ ⟧c ) underset(x - 4)(lim) ⟦x - 3⟧ ⟦ ⟧
h x = sgn x - U x Lembrando que sgn x é definido como sgn x = - 1 s e x0 0 s e x = 0 1 s e x0 E U x é a função escada definida por U x = 0 s e x0 1 s e x ≥ 0 Ache, se existirem: a ) lim x → 0 +
Dada f (x) = {[[3,x,+,2,s,e,x,,4],[5,x,+,k,s,e,4,=,x]]) Ache o valor de k para o qual o underset(x - 4)(lim) f (x) existe.