Enunciado
Cálculo - Cálculo Volume 1 - 8ª Edição - James Stewart- Ed: 8º - Capítulo 2.6 - Ex. 10
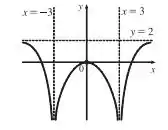
Esboce o gráfico de um exemplo de uma função que satisfaça todas as condições dadas
Passo 1
Bom galera, para resolver esse exercício, iremos elaborar um gráfico que satisfaça todas as condições apresentadas.
Iremos utilizar dos nossos conhecimentos relacionados a como os limites afetam um gráfico.
Passo 2
Para que satisfaça a condição
O nosso gráfico deverá ter no eixo o valor de conforme se aproxima de . Isso significa que a função deverá crescer indefinidamente a valores grandes, porém negativos, a medida que nos aproximamos de .
Para que satisfaça a condição
O nosso gráfico deverá ter no eixo o valor de conforme se aproxima de. Agora o que teremos então é nos aproximarmos a 2 a medida que os valores de se tornam grandes.
Passo 3
Para que satisfaça a condição
O nosso gráfico deverá ter no eixo o valor de quando for .
Para que satisfaça a condição
O nosso gráfico deverá ser simétrico em relação ao eixo .
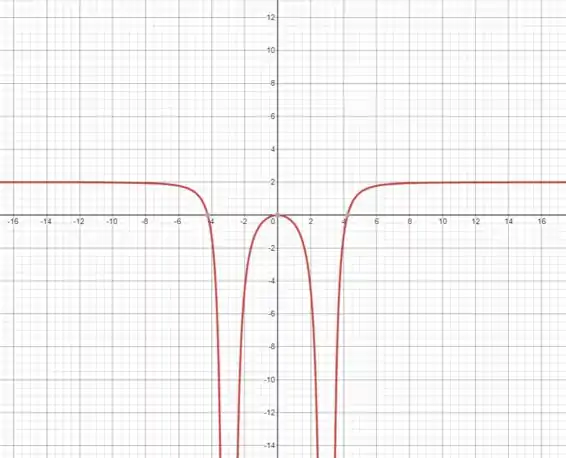b
Resposta
