Enunciado
Cálculo - Cálculo com Geometria Analítica Volume 1 - 3ª Edição - Louis Leithold- Ed: 3º - Capítulo 2.4 - Ex. 37
Para cada uma das funções a seguir, ache a assíntota vertical do gráfico e faça um esboço dele:
Passo 1
A assíntota vertical é o valor de que ao tomarmos o limite ele vai para ou para .
Para acharmos essas assíntotas, precisamos calcular o limite em alguns candidatos.
Quem são eles?
Como aqui temos uma fração, os candidatos serão os que zeram o denominador.
Nesse caso
Para o cálculo da assíntota, devemos separar nos limites laterais, para entender o comportamento da função. Ou seja, calcular
E
Passo 2
Começando com
Que vai ser
Opa, deu um número sobre . Então esse limite vai para ou para . Basta olharmos o sinal de próximo de , neste caso, pela direita.
Pela direita, significa pegar valores maiores que , logo o nosso denominador, que é , vai assumir valores maiores que , sendo positivo.
Mas temos o no denominador, isso vai fazer com que fique negativa.
E isso nos diz que
Passo 3
Começando com
Que vai ser
Opa, deu um número sobre . Então esse limite vai para ou para . Basta olharmos o sinal de próximo de , neste caso, pela esquerda.
Pela esquerda, significa pegar valores menores que , logo o nosso denominador, que é , vai assumir valores menores que , sendo negativo.
Mas temos o no denominador, isso vai fazer com que fique positiva.
E isso nos diz que
Passo 4
Como achamos pelo menos um dos limites laterais indo para , nessa questão os dois né rs
Temos que
É assíntota vertical.
Separamos os limites laterais para conseguirmos esboçar o gráfico corretamente.
Porque quando chegar próximo de por valores ele sobre indefinidamente, e quando ele estiver um pouco depois, ou seja, por valores maiores ele vai decrescer indefinidamente.
O esboço vai ficar
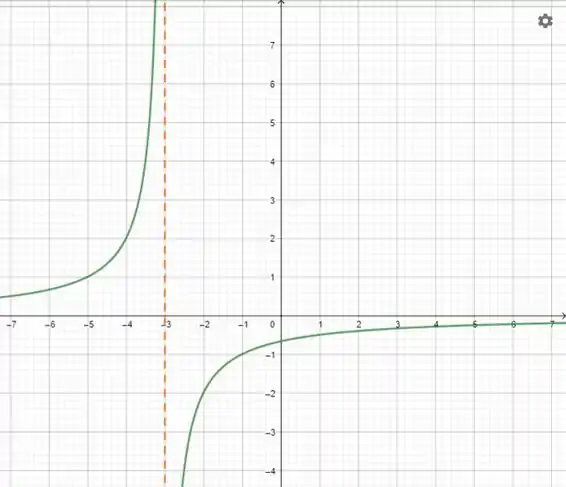
Repara que antes do a função sobe loucamente.
E depois do ela vem lááááá do
Resposta
Assíntota vertical:
