Encontre uma fórmula para uma função que satisfaça as seguintes condições:

Um belo primeiro chute pra seria:

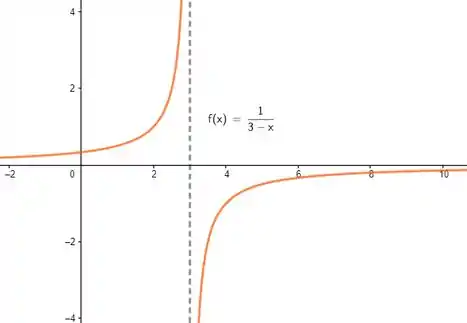
Pra garantir a assíntota, bastava a gente criar uma situação problemática na função! Nesse caso, veja que se , temos , o que não existe! Outras duas coisas importantes de notar no nosso chute inicial:

1. Se tentarmos algo do tipo , garantimos também as assíntotas, porém faremos os limites laterais de pra tenderem ambos pra , o que não é o dado do enunciado;
2. Se tentarmos algo do tipo , apesar de garantirmos que os limites laterais darão infinitos diferentes, acharíamos ao invés de como o enunciado quer!

Boa galera, agora que temos um chute inicial que já garante pra gente das condições do enunciado, vamos pensar nas próximas condições. Veja que temos do enunciado:

Com o nosso chute, por enquanto, temos:

Pô, o denominador pra vira , o que facilita nossa vida. Mas o numerador é ! Ele devia dar zero! Pra isso ser possível, que tal a modificação:

O gráfico fica:

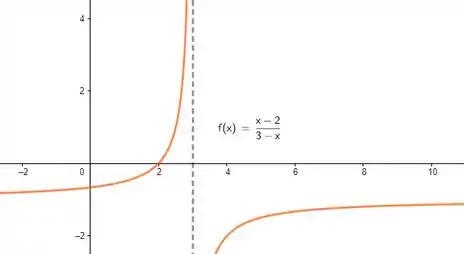
Note que a escolha de apesar de também garantir faria com que os limites laterais pra se invertessem!!!

Beleza, vamos continuar. Veja que o limite:

Implica que pode ser entendido como uma divisão de polinômios onde o do denominador tem grau maior! E mais! Nos mostra que é uma assíntota horizontal! Além disso, o limite que falta a gente verificar:

Representa uma assíntota vertical! Portanto devemos modificar de forma a gerar essa assíntota vertical e ao mesmo tempo a fazer o grau do polinômio do denominador ser maior. Um bom primeiro chute é:

O gráfico fica:

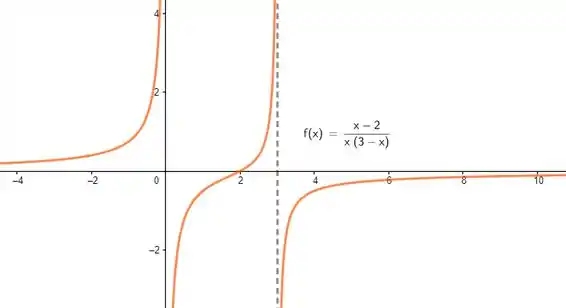
Essa escolha inicial é um pouco problemática, pois apesar de termos garantido a nova assíntota vertical e a assíntota horizontal, achamos limites laterais diferentes pra , e eramos pra achar limites iguais! Isso acontece porque:

Note que o limite restante tem resultado diferente dependendo do caminho de aproximação de pra :

E logo:

Então devemos fazer uma última modificação na nossa função pra resolver esse problema.

Veja que se fizermos:

Com gráfico:

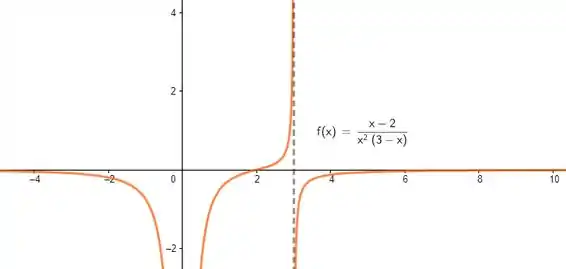
Resolvemos nosso problema anterior. Afinal, a assíntota vertical e a horizontal continuam mantidas! A diferença é que o limite que calculamos passa a ser:

Como:

E logo:

Então ta fechadinho! Nos certificamos de que os dois limites laterais pra deram infinitos iguais e negativos, confirmando o limite do enunciado:

Ao multiplicarmos o do passo anterior por , modificamos a função aumentando o grau do polinômio no denominador, o que não atrapalha a gente em nada e o limite:

Continua valendo! E era isso que faltava galera, afinal as outras condições do enunciado

Foram confirmadas no passo e . A expressão final de é: