Enunciado
Cálculo - James Stewart - Vol 1- Ed: 8º - Capítulo 1.2 - Ex. 28
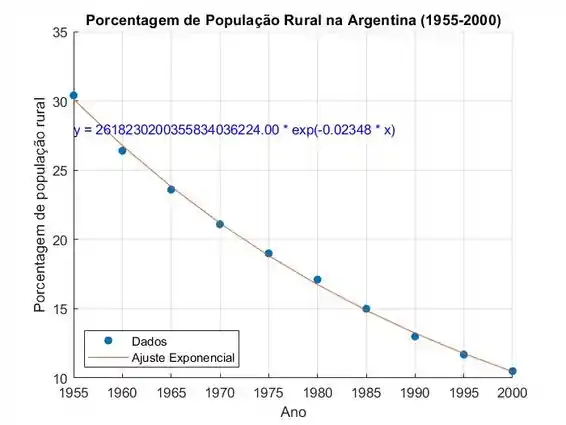
A tabela mostra a porcentagem da população da Argentina que vivia em áreas rurais de 1955 a 2000. Encontre um modelo para os dados e use-o para estimar a porcentagem de população rural em 1988 e 2002.
Passo 1
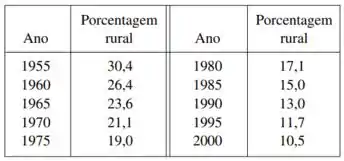
Eaeee, belezinha?? Bom... A questão fornece uma tabela com a porcentagem da população argentina que vivia em áreas rurais em diferentes anos:
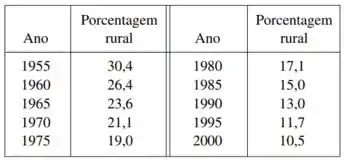
A partir dos dados da tabela, queremos encontrar um modelo e estimar a porcentagem de população rural em 1988 e 2002.
Para isso, devemos colocar os pontos em um gráfico e depois ligar os pontos.
Com uma calculadora gráfica, teremos poderemos estimar uma função a respeito dos valores indicados.
E aí?? Bora lá?? ����
Passo 2
A seguir plotamos os pontos num diagrama de dispersão pelo excel, e também conseguimos obter a equação que iremos utilizar:
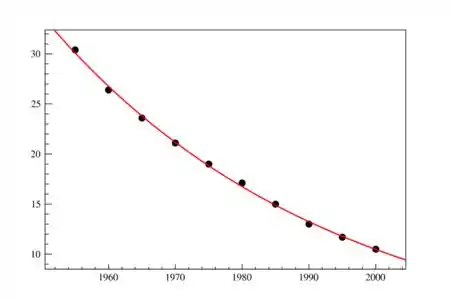
Aparentemente trata-se de um modelo exponencial decrescente deve descrever esses dados.
Passo 3
Vamos tentar um ajuste do tipo
Coloquei para definir como o valor de onde que é nossa origem de tempo!
Fazendo o ajuste:
Os valores encontrados para os parâmetros do ajuste são
Portanto, temos a nossa função:
Passo 4
Assim, para estimar a porcentagem de população rural em 1988 e 2002, basta substituirmos o valor de por esses anos.
Para :
Já para :
Passo 5
De combãooo, o RA vai dar uma colher de chá enormeee,
Vamos resolver a questão por codigo de matlab, e mostrar como os valores batem:
% Dados
anos = [1955, 1960, 1965, 1970, 1975, 1980, 1985, 1990, 1995, 2000];
porcentagem_rural = [30.4, 26.4, 23.6, 21.1, 19, 17.1, 15, 13, 11.7, 10.5];
% Ajuste exponencial
coeficientes_exponencial = polyfit(anos, log(porcentagem_rural), 1);
a = exp(coeficientes_exponencial(2));
b = coeficientes_exponencial(1);
% Estimativa da porcentagem de população rural em 1988 e 2002
ano_1988 = 1988;
ano_2002 = 2002;
porcentagem_1988 = a * exp(b * ano_1988);
porcentagem_2002 = a * exp(b * ano_2002);
fprintf('Estimativa da porcentagem de população rural em 1988: %.2f%%\n', porcentagem_1988);
fprintf('Estimativa da porcentagem de população rural em 2002: %.2f%%\n', porcentagem_2002);
% Plotar os dados e o ajuste exponencial
figure;
scatter(anos, porcentagem_rural, 'filled');
hold on;
grid on;
xlabel('Ano');
ylabel('Porcentagem de população rural');
title('Porcentagem de População Rural na Argentina (1955-2000)');
plot(anos, a * exp(b * anos));
% Adicionar a equação da função exponencial no gráfico
equacao_exponencial = sprintf('y = %.2f * exp(%.5f * x)', a, b);
text(1955, 28, equacao_exponencial, 'FontSize', 10, 'Color', 'blue');
% Adicionar a legenda
legend('Dados', 'Ajuste Exponencial', 'Location', 'southwest');
Passo 6
Agora vamos apresentar a saída do matlab, confirmando o que fizemos e o gráfico
