Enunciado
Cálculo - Cálculo com Geometria Analítica Volume 1 - 3ª Edição - Louis Leithold- Ed: 3º - Capítulo 3.8 - Ex. 40
40. Há duas reats que passam pelo ponto (-1,3) que são tangentes à curva Ache as equações de cada uma delas.
Passo 1
Nesta questão o enunciado nos pede para determinarmos a equação de duas restas tangente à curva no ponto dado. Para isso, devemos saber que a equação da reta tangente tem a seguinte forma : y = ax + b, em que a é o coeficiente angular e pode ser obtido a partir da derivada da função dada no enunciado e b é o coeficiente linear e pode ser obtido após encontrar a, substituindo os valores do ponto dado no enunciado.
Uma equação de reta tangente pode ser obtida fazendo y como função de x e a outra reta tangente pode ser obtida fazendo x como função de y.
Para derivar a função em questão pode-se utilizar do conceito de derivação implícita, que é mais uma técnica a ser utilizada para encontrarmos a derivada de uma dada função. Esta técnica é bem útil quando estamos diante de funções em que não é possível isolar y em função de x ou vice – versa.
Para resolver questões por derivação implícita basta seguir os seguintes itens
- Derivar ambos os lados da igualdade, utilizando técnicas de derivação como a regra da cadeia, regra do produto e do quociente;
- Ao lado de cada derivada encostar uma fracão d_/d_ em que no espaço vazio do denominador você fixa uma variável e no espaço vazio do numerador você coloca a variável na qual acabou de derivar;
- Após o passo anterior basta isolar, por meio de operações matemáticas básicas, o que está sendo pedido no enunciado.
Passo 2
Como dito anteriormente, o coeficiente angular ( a ) é obtido a partir da derivada da função dada no problema, sendo assim
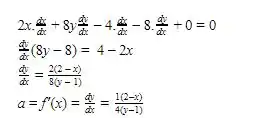
Passo 3
Aplicando o ponto dado (-1,3) na expressão de (a) para encontrar o seu valor neste ponto temos
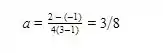
Então, até agora temos que a equação da reta tangente à curva no ponto está da seguinte forma
Passo 4
Substituindo o ponto (-1,3) na equação da reta obtida até o momento para encotrar o valor de b
Assim , a equeção da reta tangente à curva (fazendo y como função de x) no ponto (-1,3) é
Para obter a outra equação da reta tangente à curva no ponto dado basta encontrar dx/dy na expressão dada e repetir os mesmos passos anteriores.
Passo 5
Como dito anteriormente, o coeficiente angular ( a ) é obtido a partir da derivada da função dada no problema, sendo assim
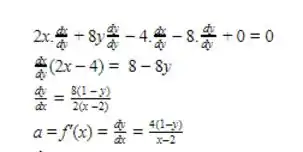
Passo 6
Aplicando o ponto dado (-1,3) na expressão de (a) para encontrar o seu valor neste ponto temos
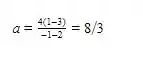
Então, até agora temos que a equação da reta tangente à curva no ponto está da seguinte forma
Passo 7
Substituindo o ponto (-1,3) na equação da reta obtida até o momento para encotrar o valor de b
Assim , a equeção da reta tangente à curva (fazendo x como função de y) no ponto (-1,3) é