Enunciado
Cálculo - James Stewart - Vol 1- Ed: 8º - Capítulo 2.7 - Ex. 26
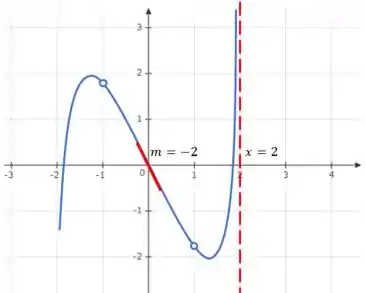
Esboce o gráfico de uma função que é continua no domínio e onde é contínua para todos os números no domínio, exceto e é impar.
Passo 1
Fala aí! tudo certinho? 😊
Nesse problema nosso objetivo é esboçar o gráfico de uma função continua no intervalo exceto em sendo que e .
E como ele não nos dá a lei de formação da função, vamos analisar cada pedacinho das características ditas pelo enunciado.
E traçar uma função que respeita todas essas características. Ou seja, a ideia aqui é ir construindo uma curva genérica que obedeça às regrinhas dadas
Tem ideia de como fazer isso? Vem que te ajudo 🤔
Passo 2
Bom pessoal, vamos começar esboçando partes do gráfico.
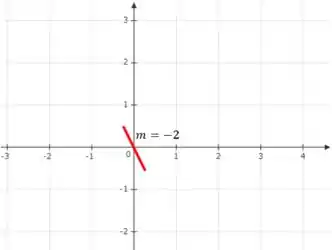
Temos que:
Isto é, a inclinação da tangente da curva no ponto em que é .
Ou seja, ela será decrescente ao cortar o eixo , e sua reta tangente tem inclinação é de .
Outra informação que o enunciado também nos dá é de que é uma função ímpar. Então ela passará pela origem do eixo cartesiano.
Como ainda temos pouca informação sobre ela, vou desenhar aqui só a reta tangente a ela na origem.
Passo 3
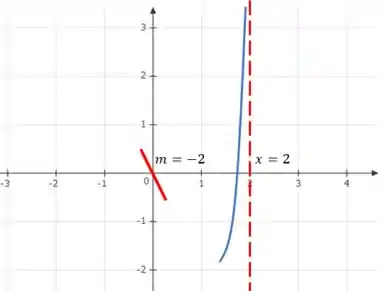
A próxima informação que vamos usar é a de que:
Quando um limite vai para o infinito em um valor específico de , temos uma assíntota vertical. Ou seja, a função se aproxima de uma reta vertical que corta o eixo naquele ponto específico.
Para esse caso em pela esquerda, com a curva subindo até infinito.
Passo 4
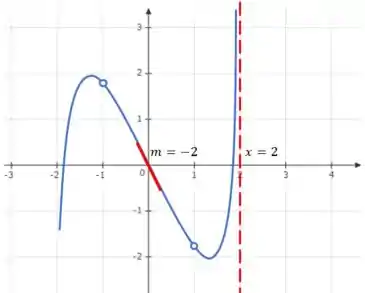
O enunciado também nos diz que a função que é continua no domínio exceto e é ímpar. Então vamos completar a curva que já temos deixando um buraco nela para
Lembrando que é ímpar, então a função pode ter as seguintes características...
E aí! entendeu? Responde Aí! 😉
Resposta
