Enunciado
Cálculo - Cálculo com Geometria Analítica Volume 1 - 3ª Edição - Louis Leithold- Ed: 3º - Capítulo 3.8 - Ex. 43
Nos Exercicicios de 41 a 46, é dada uma equação. Faça o seguinte em cada um destes problemas: (a) Ache duas funções definidas pela equação equação e estabeleça os seus domínios. (b) Faça um esboço do gráfico de cada uma das funções obtidas na parte (a). (c) Faça um esboço gráfico da equação. (d) Ache a derivada de cada uma das funções obtidas na parte (a) e estabeleça seus domínios. (e) Ache por derivação implícita da equação dada e comprove que o resultado assim obtido está de acordo com a parte (d). (f) Ache uma equaçãi da reta tangente em cada valor dado de
43.
Passo 1
Nesta questão, não tem muito o que extrair do enunciado, basta apenas reproduzir o que está sendo pedido em cada letra para chegar na resposta. Porém, devemos está atentos nas letras (d) e (e) onde são utilizado os conceitos de derivada e derivada implícita,respectivamente.
Na hora de resolver o item (d) deve – se atentar que Para derivar a função em questão pode-se utilizar do conceito de derivação implícita, que é mais uma técnica a ser utilizada para encontrarmos a derivada de uma dada função. Esta técnica é bem útil quando estamos diante de funções em que não é possível isolar y em função de x ou vice – versa.
Para resolver questões por derivação implícita basta seguir os seguintes itens
- Derivar ambos os lados da igualdade, utilizando técnicas de derivação como a regra da cadeia, regra do produto e do quociente;
- Ao lado de cada derivada encostar uma fracão d_/d_ em que no espaço vazio do denominador você fixa uma variável e no espaço vazio do numerador você coloca a variável na qual acabou de derivar;
- Após o passo anterior basta isolar, por meio de operações matemáticas básicas, o que está sendo pedido no enunciado.
Passo 2
Letra (a)
Passo 3
Letra (b)
Gráfico de
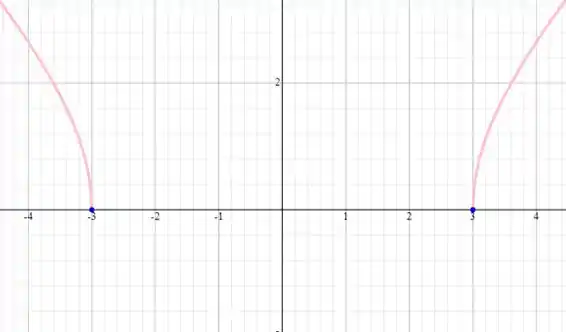
Gráfico de
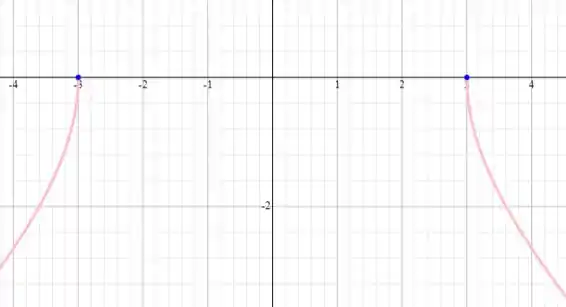
Passo 4
Letra (c)
Esboço do gráfico da equação
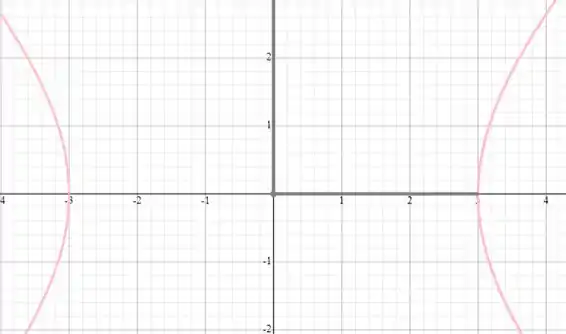
Passo 5
Letra (d)
A Derivada e o respectivo domínio de e é igual a
Passo 6
Letra (e)
Encontrando dy/dx por derivação implícita temos
Se y = , então
Se y = , então
Passo 7
Letra (f)
Como sabemos que o coeficiente angular da reta tangente é igual a a = f´ (x) = dy/dx e que reta tangente apresenta a seguinte equação : Y = ax + b , podemos encontrar qual é a reta tangente a curva dada no valor de x1.
Se x1 = -5 , então y = . Assim, aplicamos um dos valores de y na derivada obtida implicitamente para encontrar o valor de a no ponto.
Então, até agora temos que a equação da reta tangente à curva no ponto está da seguinte forma
Passo 8
Substituindo o ponto na equação da reta obtida até o momento para encotrar o valor de b
Assim , a equeção de uma das retas tangentes à curva no ponto (-5,4) é
A outra equação da reta tangente pode ser obtida substituindo o outro valor de y na derivada obtida implicitamente e repetindo as mesmas etapas seguidas para encontrar a reta acima.
Resposta
(a)
(b) gráfico
(c) gráfico
(d)
(e) 
(f)