Enunciado
Cálculo - Cálculo Volume 2 - 8ª Edição - James Stewart- Ed: 8º - Capítulo 14.1 - Ex. 27
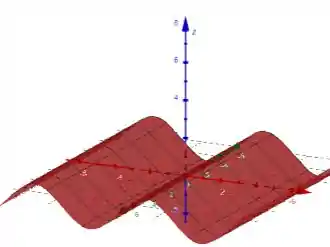
Esboce o gráfico da função.
Passo 1
Eaee, tudo bem?? Bom... queremos esboçar o gráfico da seguinte função:
Para isso, precisamos saber que a função está na forma:
Além disso, precisamos saber também que, como trata-se de uma função linear de duas variáveis , o gráfico desse tipo de função é um plano no espaço tridimensional.
Uma dica é analisar a função fazendo uma das variáveis indo para zero e depois fazer a mesma coisa para a outra variável.
Agora bora lá!! 😉
Passo 2
Bom... da nossa função, temos:
Opa!!! A função é bem conhecida!!
Veja que, como não foi definida, temos que é todo o plano real!!
Com isso, basta fazermos a função e estender para a forma tridimensional da seguinte forma:
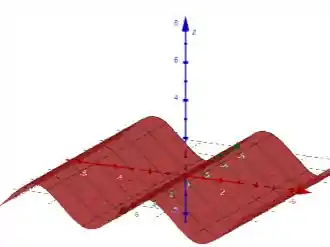
Perceba que se analisássemos apenas os eixos , veríamos uma senóide.
Resposta
Exercícios de Livros Relacionados
Desenhe as curvas de nível e determine a imagem.f (x , y) = x y
Desenhe as curvas de nível e determine a imagem.f (x , y) = (y)/(x - 2)
Desenhe as curvas de nível e determine a imagem.f (x , y) = 3 x^2 - 4 x y + y ² ²
Desenhe as curvas de nível e determine a imagem.f (x , y) = (x ²)/(x^2 + y ²) ² ²
Desenhe as curvas de nível e determine a imagem.f (x , y) = 4 x^2 + y ² ²