Enunciado
Cálculo - James Stewart - Vol 1- Ed: 8º - Capítulo 2.8 - Ex. 62
Esboce o gráfico da função . Para que valores de é diferenciável? Encontre uma fórmula para .
Passo 1
Fala aí! tudo certinho?
Nesse problema foi dada a função
E nosso objetivo é dizer para quais valores de a função é diferenciável e tambem queremos obter uma formula para .
Parece complicado?
Bom galera, primeiro a gente pode observar que por causa do módulo a função tem duas partes:
Quando , os termos da função se cancelam e quando , os termos da função se somam...
Dessa forma podemos rescrever nossa função como
Agora como temos uma função definida por partes, podemos resolver nosso problema de maneira mais simples.
Veja só!
Passo 2
Se esboçarmos o gráfico de , vemos que em a função é constante e igual a , mas para a função é uma reta ...
Com isso, temos
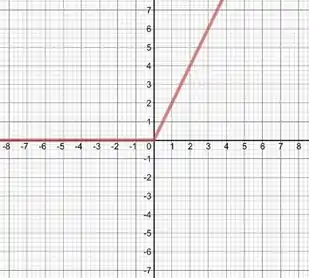
Lembra que quando temos um bico em um ponto da função, esse ponto não é diferenciável?
Aqui temos um bico em , então a partir do gráfico, devido a junção das duas retas a função não é diferenciável em .
Então ela é diferenciavel para todo .
Show de bola?
Passo 3
Agora queremos determinar uma formula para ...
Sabemos que a derivada de uma função pode ser interpretada como a inclinação da reta tangente a essa função...
Portanto, como temos duas retas que compõe a função, podemos definir como as inclinações de cada uma das partes...
Escrevendo isso em função de temos que se , . Mas se , e em a não não está definida...
Usando o módulo também podemos escrever:
É isso! O que achou? Responde Aí!
Resposta
É diferenciavel para todo