Enunciado
Cálculo - James Stewart - Vol 1- Ed: 8º - Capítulo 2.8 - Ex. 38
A temperatura da água afeta a taxa de crescimento da truta. A tabela mostra a quantidade de peso adquirida pela truta após dias em várias temperaturas da água. Se for o ganho de peso na temperatura , construa uma tabela dos valores estimados para e esboce seu gráfico. O que são as unidades para ?
Passo 1
Fala galera, tudo bem? O problema nos deu uma tabela que mostra valores de temperatura e peso ganho para um espécie de peixe. O problema pede para encontrarmos os valores estimados de , mas o que seria isso?
Seria a taxa de ganho de peso! Ganho esse de peso em função da temperatura! Vamos chamar temperatura de e ganho de peso , e sabemos que taxa é a razão entre duas grandezas, assim o ganho (ou a estimativa de) para uma variação de temperatura é
Podemos também relacionar com o conceito de derivada! Derivada é sempre a inclinação de uma função, considerando isso é a divisão da variação da imagem pela variação do domínio! Vamos chamar o domínio de e imagem de . Beleza?
A ideia é relacionar a ideia de derivada com estimativa para achar o que se pede! Mas uma coisa já podemos pensar sobre: a unidade!
É o ganho de peso (medido em gramas) pela variação de temperatura (medida em ) certo? Então a taxa é a razão dessas unidades
E o restante? Calma, vamos fazer aos poucos! Vem comigo!
Passo 2
A diferença crucial entre derivada e estimativa é o intervalo entre medidas considerado! Quando temos uma estimativa é porque o intervalo (no nosso caso) de temperatura não é tão pequeno assim, como se fosse a velocidade média em um carro.
Essa estimativa vai, como o nome diz, estimar o valor da taxa de ganho de peso, mas não será tão preciso quanto a derivada.
Já para determinar a derivada, precisamos de uma função que descreva bem o comportamento. Como na velocidade instantânea: a gente sabe exatamente como se comporta a posição em função do tempo, e portanto, podemos derivar e achar a velocidade instantânea!
Assim teremos uma informação em tempo real da velocidade, ou no nosso caso, do ganho de peso na temperatura exata.
Beleza?
Passo 3
Beleza, agora vamos contruir uma tabela com estimativas para os valores de .
Podemos calcular a derivada estimada em cada uma das temperaturas, entre e :
Veja que os valores são próximos, mas não muito! Isso porque não temos uma função analítica para o peso em função da temperatura.
Para os outros anos iremos usar uma média entre a aproximação pelos dois lados, começando por :
Considerando isso, a média dos dois é a seguinte:
Passo 4
Repetindo o passo anterior para os outros anos, obtemos a seguinte tabela:
Passo 5
Show de bola, agora iremos pegar os pontos de e colocar em um gráfico, como mostrado abaixo, considerando que temos uma razão entre peso e temperatura, teremos a unidade de medida igual a .
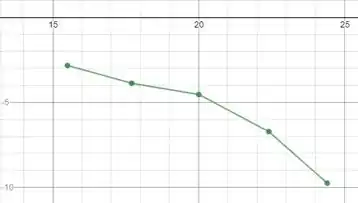
No eixo vertical seria o ganho de peso e na horizontal a temperatura.
Beleza? Espero ter ajudado!