Enunciado
Cálculo - Cálculo Volume 1 - 5ª Edição - James Stewart- Ed: 5º - Capítulo 2.9 - Ex. 45
45.
(a) Esboce o gráfico da função .
(b) Para que os valores de são diferenciáveis?
(c) Encontre uma fórmula para
Passo 1
Inicialmente transformaremos nossa função em uma função de duas variáveis:
Se ,
Então
Se ,
Então
O gráfico para é um ramo de parábola com concavidade voltada para cima.
E para , é um ramo de parábola com concavidade para baixo. Faremos o esboço no próximo passo.
Passo 2
(A)
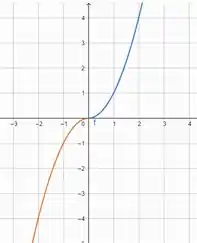
(B)
A função não apresenta bico, nem tangente vertical e nem descontinuidade, então é derivável em todos os valores Reais.
Passo 3
(C)
Na letra c, usaremos a fórmula de derivada para calcularmos, mas faremos duas expressões, uma para e outra para :
Para :
Para :
Resposta
(A)
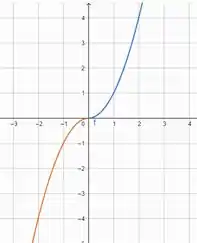
(B)
A função não apresenta bico, nem tangente vertical e nem descontinuidade, então é derivável em todos os valores Reais.
(C)