Enunciado
Cálculo - Cálculo com Geometria Analítica Volume 1 - 3ª Edição - Louis Leithold- Ed: 3º - Capítulo 3.2 - Ex. 23a
23. Dada . (a) Prove que é contínua em (b) Prove que nem nem existem. (c) Faça um esboço do gráfico de
Letra (a)
Passo 1
O enunciado fornece a função f e o intervalo ( -∞,-3] e [3,+∞) e solicita que mostremos que a função é contínua nestes 2 intervalos.
Devemos lembrar então que uma função é contínua em um determinado ponto se o limite for igual ao valor da função no ponto. Para que ela seja contínua em todo intervalo, ela deve estar definida em todos os pontos do intervalo.
Passo 2
O termo da raiz não pode ser negativo, de modo que para função estar bem definida devemos ter x2 – 9 ≥ 0. Assim, f só estaria bem definida se x2 ≥ 9.. Assim, em todos os pontos do intervalo a função está bem definida.
Passo 3
Tomemos a Є ( -∞,-3] e b Є [3,+∞). Como a ≤ -3 e b ≥ 3 , segue que
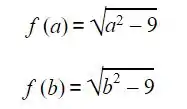
Calculemos agora o limite:
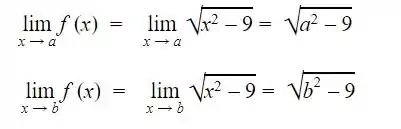
Vemos então que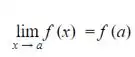 
para um x = a arbitrário pertencendo ao intervalo a ≤ -3 e um x = b arbitrário pertencendo ao intervalo b ≥ 3 . Como a e b são arbritários, a relação vale para todos os pontos do intervalo, de modo que a função é contínua no intervalo todo.
Resposta
Demonstração.