Enunciado
Cálculo - Cálculo Volume 1 - 5ª Edição - James Stewart- Ed: 5º - Capítulo 6.1 - Ex. 29
Avalie a integral e interprete-a como a área de uma região. Esboce a região.
Passo 1
Vamos lá, precisamos lidar com aquele módulo dentro da integral. É importante lembrar da definição do módulo:
Então vamos dividir nossa integral em dois trechos, um com e outro com :
No trecho positivo, nós vamos tirar o módulo e manter o sinal. No trecho negativo, nós vamos tirar o módulo e trocar o sinal:
Passo 2
Agora vamos resolver cada uma dessas integrais. Começando pela integral do trecho negativo:
E agora a intgral do trecho positivo:
Então a integral é:
Passo 3
Agora falta fazer um esboço da região. A melhor forma de fazer isso é começar com um esboço da seguinte função bem conhecida:
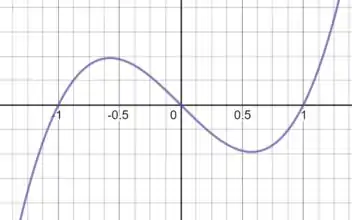
E então “jogar tudo” para o lado de cima, já que o módulo vai trocar o sinal de tudo o que é negativo:
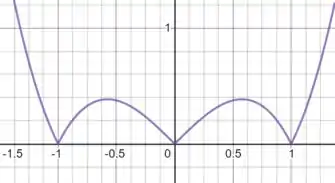
Resposta
O valor da integral é . Ver esboço.