Esboce o gráfico do integrando e use áreas para calcular a integral

Vamos começar por determinar o intervalo de análise. O intervalo será dado por , em que é o limite inferior da nossa integral e o limite superior. Desta forma, temos:

Vamos obter agora o gráfico da nossa função. Portanto, temos:

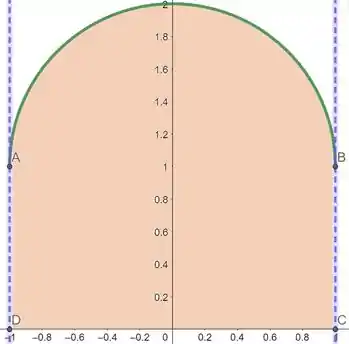
Em destaque temos a área da região que devemos calcular. Ela pode ser dividida em duas áreas: um retângulo de vértices , , e . Já a parte superior corresponde a um semicírculo de raio igual a 1 e centro no ponto . Poderíamos ter percebido que o mesmo corresponde a um semicírculo se fizermos a uma translação vertical da função em uma unidade para cima. Como a função representa um semicírculo superior de raio 1 e centrado na origem, após fazermos a translação, obteremos a nossa função que queremos integras! E agora? Fica fácil de visualizar se utilizarmos assuntos aprendidos aqui antes, né?

Como o nosso retângulo possui lado base igual a e altura igual a , a sua área é dada por:

Já o nosso semicírculo de raio possui a seguinte área:

Desta forma, a área total é:

Consequentemente,