Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Cálculo - Cálculo Volume 1 - 8ª Edição - James Stewart- Ed: 8º - Capítulo 4.6 - Ex. 14

Esboce o gráfico à mão, usando as assíntotas e as intersecções com os eixos, mas não as derivadas. Então, use seu esboço como um roteiro na obtenção de gráficos (com uma ferramenta gráfica) que mostrem os aspectos mais importantes da curva. Use esses gráficos para estimar os valores máximo e mínimo.

f x = 2 x + 3 2 ( x - 2 ) 5 x 3 ( x - 5 ) 2

Passo 1

Fala aí! tudo certinho?

Nesse problema foi dada a função

f x = 2 x + 3 2 ( x - 2 ) 5 x 3 ( x - 5 ) 2

E nosso objetivo é esboçar seu gráfico usando apenas as assíntotas e as intersecções com os eixos x y .

Depois estimamos os valores de máximos e mínimos da função...

Parece complicado?

Para obter as intersecções com os eixos já sabemos... fazemos x = 0 para obter o valor de y que a função cruza o eixo y e y = 0 para saber onde a função cruza o eixo x .

As assíntotas horizontais são obtidas em y = L 1 ou y = L 2 em

lim x → ∞ ⁡ f x = L 1

lim x → - ∞ ⁡ f x = L 2

As assíntotas verticais são obtidas onde x = a em que

lim x → a ⁡ f x = ± ∞

E as assíntotas obliquas são obtidas em

lim x → ∞ ⁡ f x + m x + c = 0

Show? Bora começar!

Passo 2

Vamos começar fazendo x = 0

f 0 = 2 0 + 3 2 0 - 2 5 0 3 0 - 5 2 = - 288 0

Perceba que aqui a função não está definida (onde pode ser uma forte candidata a assíntota vertical...)

Fazendo f x = 0

2 x + 3 2 ( x - 2 ) 5 x 3 ( x - 5 ) 2 = 0 → x = - 3 2 x = 2

Até aqui vemos que f x não corta o eixo y , mas corta o eixo x em x = - 3 / 2 e em x = 2 ...

Tranquilo até aqui?

Passo 3

Agora vamos ver se f x possui assíntotas horizontais...

lim x → ∞ ⁡ 2 x + 3 2 x - 2 5 x 3 x - 5 2 = ∞ ∞

Como estamos lidando com x tendendo a valores muito grandes, vamos considerar 2 x + 3 = 2 x , x - 2 = x e x - 5 = x

lim x → ∞ ⁡ 2 x 2 x 5 x 3 x 2 → lim x → ∞ ⁡ 4 x 7 x 5

lim x → ∞ ⁡ 4 x 2 = ∞

Agora para - ∞

lim x → - ∞ ⁡ 2 x + 3 2 x - 2 5 x 3 x - 5 2

Se fizermos a mesma aproximação, vamos chegar em

lim x → - ∞ ⁡ 4 x 2 = ∞

Então vimos que f x não possui nenhuma assíntota horizontal...

Bacana, não é?

Passo 4

Agora vamos analisar as assíntotas verticais...

Analisando a função

f x = 2 x + 3 2 x - 2 5 x 3 x - 5 2

Podemos imaginar que em x = 0 e em x = 5 tenhamos assíntotas verticais pois são os pontos onde nosso denominador zera...

Vamos analisar primeiro para x = 0

lim x → 0 ⁡ 2 x + 3 2 x - 2 5 x 3 x - 5 2 = - 288 0

Aqui como o numerador não zerou, podemos assimilar que estamos dividindo um número grande e negativo por um número muito pequeno e quase nulo... mas perceba que o termo que zera o denominador em x = 0 é x 3 ... aqui temos que tomar cuidado com o sinal:

Se x → 0 + a função tende a - ∞ pois o numerador é negativo

Se x → 0 - a função tende a ∞ .

lim x → 0 + ⁡ f x = - ∞

lim x → 0 - ⁡ f x = ∞

Então em x = 0 temos uma assíntota.

Concorda?

Passo 5

Agora vamos analisar o ponto x = 5

lim x → 5 ⁡ 2 x + 3 2 x - 2 5 x 3 x - 5 2 = 41067 0

A análise que fizemos no passo anterior vale aqui também... a única diferença é que agora o termo que zera o denominador em x = 5 nunca é negativo pois está elevado ao quadrado.

lim x → 5 + ⁡ 2 x + 3 2 x - 2 5 x 3 x - 5 2 = ∞

lim x → 5 - ⁡ 2 x + 3 2 x - 2 5 x 3 x - 5 2 = ∞

Maravilha! Encontramos mais uma assíntota!

Estamos quase lá!

Passo 6

Vamos verificar agora se temos alguma assíntota oblíqua...

Para x → ∞

lim x → ∞ ⁡ 2 x + 3 2 x - 2 5 x 3 x - 5 2 + m x + c = 0

lim x → ∞ ⁡ 2 x + 3 2 x - 2 5 + m x + c x 3 x - 5 2 x 3 x - 5 2 = 0

Novamente vamos fazer aquele esqueminha de simplificação...

lim x → ∞ ⁡ 2 x 2 x 5 + m x + c x 3 x 2 x 3 x 2 = 0

lim x → ∞ ⁡ 4 x 7 + m x + c x 5 x 5 = 0

Vamos dividir o numerador e o denominador por x 5

lim x → ∞ ⁡ 4 x 7 x 5 + m x + c x 5 x 5 x 5 x 5 = 0

lim x → ∞ ⁡ 4 x 2 + m x + c = 0

Perceba que não podemos ter uma reta palpável pois m vai tender a ∞

Então não temos assíntotas obliquas, mas vimos que f x tende a ∞ muito rápido.

Show?

Passo 7

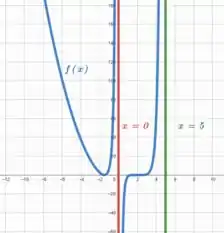
Esboçando o gráfico, temos

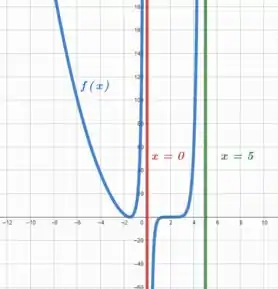
Como f x tende a ∞ em x → 0 - e x → - ∞ podemos estimar um ponto mínimo em algum valor próximo de x = - 3 2 .

E aí! o que achou? Responde Aí!

Resposta

Em x = 0 e em x = 5 a função possui assíntotas verticais e não possui assíntotas horizontais.   f ( x ) Intercepta o eixo x em - 3 2 e em 2 .

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

24. Use o método de Newton para encontrar todas as raízes da equação com precisão de oito casas decimais. Comece fazendo um gráfico para encontrar a aproximação inicial x 5 - 3 x 4 + x 3 - x 2 - x + 6
Encontre as assíntotas verticais e horizontais.Encontre os intervalos nos quais a função é crescente ou decrescente.Encontre os valores máximos e mínimos locais.Encontre os intervalos de concavidade e
Encontre os intervalos em que a função é crescente ou decrescente.Encontre os valores máximo e mínimo locais. Encontre os intervalos de concavidade e pontos de inflexão. Use as informações de a)-c) pa
Encontre os intervalos em que a função é crescente ou decrescente.Encontre os valores máximo e mínimo locais. Encontre os intervalos de concavidade e pontos de inflexão. Use as informações de a) - c)
Encontre os intervalos em que a função é crescente ou decrescente.Encontre os valores máximo e mínimo locais. Encontre os intervalos de concavidade e pontos de inflexão. Use as informações de a)-c) pa