Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Cálculo - Cálculo Volume 1 - 8ª Edição - James Stewart- Ed: 8º - Capítulo 3.5 - Ex. 80

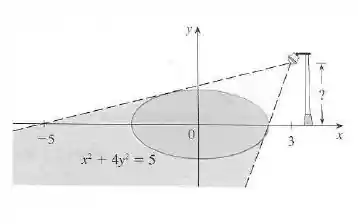
A figura mostra uma lâmpada localizada três unidades à direita do eixo y e uma sombra originada pela região elíptica x 2 + 4 y 2 ≤ 5 . Se o ponto ( - 5 ,   0 ) estiver na borda da sombra, qual a altura da lâmpada acima do eixo x ?

Passo 1

Fala, galera! Beleza? Vamos resolver essa questão!

O enunciado pediu pra gente descobrir a altura da lâmpada acima do eixo x , sabendo que ela está localizada três unidades à direita do eixo y e uma sombra originada pela região elíptica x 2 + 4 y 2 ≤ 5 , com o ponto ( - 5 ,   0 ) na borda da sombra.

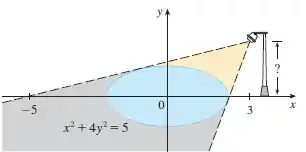
Para isso, iremos utilizar a derivação implícita para determinar a inclinação y '   da reta e usar as relações do triângulo formado pela lâmpada e sua sombra.

Vamos lá!

Passo 2

Derivando ambos os lados da equação da região elíptica, vamos ter:

x 2 + 4 y 2 = 5

2 x + 8 y y ' = 0

Isolando y ' , temos:

y ' = - x 4 y

Sendo ( a ,   b ) o ponto de encontro entre a reta que passa pelos pontos ( 3 ,   h ) e ( - 5 ,   0 ) , onde h é a altura da lâmpada, podemos encontrar a inclinação dessa reta utilizando a seguinte fórmula

m = ∆ y ∆ x = h 8

Podemos encontrar y ' utilizando a mesma fórmula. Entre os pontos ( a ,   b ) e ( - 5 ,   0 ) , temos

y ' = ∆ y ∆ x = b a + 5

Igualando a expressão obtida com

y ' = - x 4 y = - a 4 b

Temos

- a 4 b = b a + 5

a 2 + 4 b 2 = - 5 a

Passo 3

Se o ponto ( a ,   b ) pertencer a elipse, podemos escrever

x 2 + 4 y 2 = 5

a 2 + 4 b 2 = 5

Dessa forma, temos um sistema com duas incógnitas e duas equações

a 2 + 4 b 2 = 5 a 2 + 4 b 2 = - 5 a

Resolvendo o sistema, encontramos o seguinte resultado

a = - 1 e b = 1

Podemos então encontrar h com base na relação encontrada anteriormente

h 8 = b a + 5

h = 2

Sendo assim, a lâmpada se encontra 2 unidades acima do eixo.

Valeu, galera! Até a próxima! 😉

Resposta

A lâmpada se encontra 2 unidades acima do eixo.

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Encontre d y // d x por derivação implícita.2 x^3 + x^2 y - x y^3 = 2
Se x y + e^y = e , encontre o valor de y ' ' no ponto onde x = 0 .
Mostre que a elipse x 2 a 2 + y 2 b 2 = 1 e a hipérbole x 2 A 2 - y 2 B 2 = 1 são trajetórias ortogonais se A 2a 2 e a 2 - b 2 = A 2 + B 2 (logo, a elipse e a hipérbole possuem os mesmos focos).
Se x 2 + x y + y 3 = 1 , encontre o valor de y ' ' ' no ponto onde x = 1 .
Use a derivação implícita para encontrar y ' se x 2 + x y + y 2 + 1 = 0 .Trace a curva da parte (a). O que você observa? Demonstre que o que você observa está correto.Em vista da parte (b), o que você