Enunciado
Cálculo - Cálculo Volume 1 - 8ª Edição - James Stewart- Ed: 8º - Capítulo 4.1 - Ex. 17
Esboce o gráfico de à mão e use seu esboço para encontrar os valores máximos e mínimos locais e absolutos de . (Use os gráficos e as transformações das Seções 1.2 e 1.3.)
Passo 1
Fala aí, tudo certinho com você?
Bom, essa questão pede pra gente esboçar o gráfico de
à mão e usar seu esboço para encontrar os valores máximos e mínimos locais e absolutos de .
E para isso podemos lembrar que essa função é uma daquelas velhas conhecidas nossa e seu gráfico é bem usado.
Assim, a mão teremos uma ideia do comportamento da função.
Vem comigo que te mostro como.
Passo 2
Queremos esboçar o gráfico da função
Para
Assim, o gráfico será
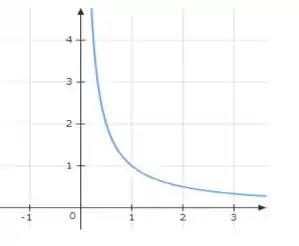
Mas limitado o intervalo dado, teremos apenas:
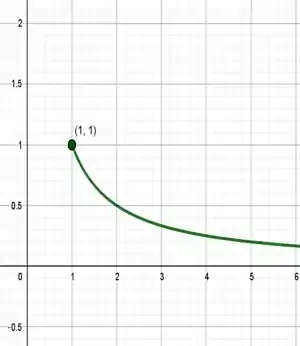
Passo 3
Vemos que o ponto máximo então é e não temos pontos mínimos, pois a função só está limitada superiormente, com a condição de que , já que ela é decrescente.
Sendo assim:
- Ponto máximo local: não tem.
- Ponto máximo absoluto:
- Ponto mínimo local: não tem
- Ponto mínimo absoluto: não tem.
Resposta
Apenas ponto máximo absoluto: