Enunciado
Cálculo - Cálculo Volume 1 - 8ª Edição - James Stewart- Ed: 8º - Capítulo 4.5 - Ex. 9
Use o roteiro dessa seção para esboçar a curva.
Passo 1
A questão pede para usarmos a roteiro apresentado na seção do livro para fazer um esboço da curva.
Assim, precisaremos encontrar:
O domínio da função, que são os valores que o pode assumir.
As interseções com eixos, que são os valores de quando e de quando .
Limites no infinito, onde faremos:
Intervalos de crescimento e os pontos críticos, onde analisaremos o sinal da derivada da função, fazendo:
Fazer um estuda da concavidade
E qualquer outra consideração que ajude a entender bem o comportamento da função.
Então vem ver tudo isso.
Passo 2
Vamos começar procurando o domínio da função, que são os valores que o pode assumir.
Perceba que sendo nossa função dada por:
O denominador não pode se anular. Então, devemos ter
Assim,
Desta forma, o domínio da função
Passo 3
Para encontrar as interseção com eixos, vamos procurar os valores de quando e de quando .
Assim, no eixo , teremos:
E no eixo , teremos:
O que só acontece se .
Com isso, a única interseção com os eixos coordenados ocorre em .
Passo 4
Vamos ver se a função é par ou ímpar.
Se
Se
Então trocando por :
E vemos que
Assim, a função não é nem par nem ímpar!
Passo 5
Vamos agora procurar possíveis assíntotas. Para indo para :
Assim, tanto para como para , a reta é assíntota horizontal da função.
Como não está no domínio da função, vamos ver se a função tem assíntota vertical nele. Fazendo os limites laterais:
Desta forma, a reta é assíntota vertical.
Passo 6
Vamos estudar agora os intervalos de crescimento e decrescimento da função. Calculando a primeira derivada:
Como
no domínio da função,
de modo que a curva é sempre descrescente. Além disso, como
a curva não tem pontos críticos.
Passo 7
Por fim, vamos analisar a concavidade da curva. Fazendo a segunda derivada:
Como o expoente é ímpar, o denominador pode ser tanto positivo como negativo:
A curva não tem pontos de inflexão por não está em seu domínio.
O esboço da curva:
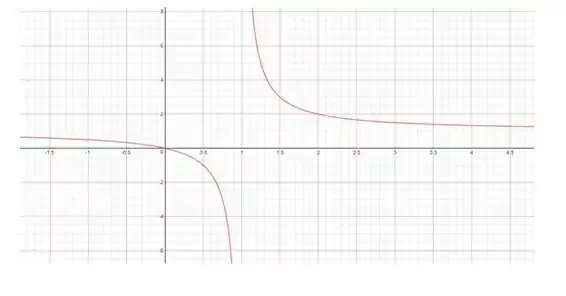
Resposta
O esboço da curva:
