Enunciado
Cálculo - Cálculo Volume 1 - 6ª Edição - James Stewart- Ed: 6º - Capítulo 4.5 - Ex. 31
Use o roteiro dessa seção para esboçar a curva.
Passo 1
Eaee, belezinha?? Bom... A questão pede para usarmos a roteiro apresentado na seção do livro para fazer um esboço da curva.
Aqui nós temos a função
E aqui vamos seguir o seguinte roteiro para esboçar o gráfico dela.
A. Encontrar o domínio em que a função é definida.
B. Encontrar os interceptos. Que são os pontos onde a função cruza o eixo , isso é:
E o pontos onde a função cruza o eixo , isso é:
C. Verificar se há simetria par, isso é:
Para isso, basta substituir por e verificar se a expressão se mantém a mesma.
D. Procurar por assíntotas horizontais e verticais.
Uma assíntota horizontal é um valor real para o qual a função tende quando tende para infinito:
Já uma assíntota vertical é um valor de no qual a função possui uma descontinuidade e tende para infinito.
E. Encontrar os intervalos de crescimento e decrescimento. Para isso, basta derivar a função e nos intervalos em que a derivada for positiva a função cresce
E nos intervalos em que a derivada for negativa a função decresce
F. Encontrar os pontos de máximo e mínimo local.
Esses pontos ocorrem quando a derivada vale zero e troca de sinal ou quando a derivada possui uma descontinuidade e troca de sinal.
Caso a derivada fosse negativa e depois do ponto ela é positiva, então a função possui um ponto de mínimo local. Se a derivada era positiva e depois do ponto ela é negativa, então a função possui um ponto de máximo local.
G. Encontrar os intervalos de concavidade e pontos de inflexão.
A concavidade é para cima se a derivada segunda for positiva
E a concavidade é para baixo se a derivada segunda for negativa
Por fim, um ponto de inflexão é um ponto onde a derivada segunda vale zero e troca de sinal.
H. Esboçar a função juntando as informações obtidas.
Assim, precisamos encontrar o domínio da função, interseção com eixos, limites no infinito, intervalos de crescimento, pontos críticos, fazer um estuda da concavidade e qualquer outra consideração que ajude a entender bem o comportamento da função.
Bora lá!! 😉
Passo 2
Como a função seno admite qualquer real, o domínio da função é real:
Passo 3
Observe que como o seno é periódico e a função dada só depende de , então a função é periódica de período .
Assim, só precisamos nos preocupar com o intervalo .
Vale observar também que a função é ímpar pois o seno é ímpar.
Passo 4
Vamos achar a interseção com eixo fazendo
Portanto, a função cruza o eixo em .
Para as raízes, temos que
Portanto, temos que
ou
(o que não é possível pois o seno deve ser menor que 1).
Assim, temos apenas que , de modo que no intervalo que estamos considerando, temos apenas e .
Logo, as interseções com os eixos são e .
Passo 5
Como se trata de uma função trigonométrica pura, não faz sentido falar em assíntotas ou analisar o comportamento no infinito: basta fazer o gráfico no intervalo e repeti-lo.
Passo 6
Vamos estudar agora o crescimento e decrescimento da curva fazendo a derivada da função:
Assim, o sinal de será dado pelo sinal de :
De forma que
Quando
No intervalo de a , isso ocorre quando
Esse é o intervalo que a derivada é positiva e portanto a função cresce.
Nos demais intervalos de a , a derivada é negativa e a função decresce. Temos portanto a seguinte tabela.
Assim, a função cresce no primeiro e quarto quadrantes, e decresce nos demais.
A função terá um máximo local em e um mínimo em .
No máximo, a função vale e no mínimo, .
Passo 7
Para a concavidade usaremos a segunda derivada:
Derivando temos:
Assim, quem vai controlar o sinal da concavidade é o seno pois .
Note que o sinal da concavidade será oposto ao sinal do seno.
Portanto,
Quando
Entre e , isso ocorre em .
Desta forma, a concavidade será para cima (positiva) no terceiro e quarto quadrantes, e para baixo (negativa) no primeiro e segundo quadrante.
São pontos de inflexão os pontos e e e por aí vai.
Passo 8
Com essas informações, temos o nosso gráfico. Repare que tivemos informações de até , para o restante basta repetir o que já encontramos por conta da periodicidade da função seno.
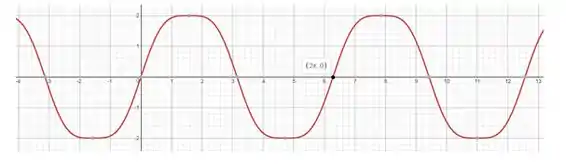
Resposta
Fazendo o gráfico no intervalo e repetindo ele para a reta real toda, temos que:
