Enunciado
Cálculo - Cálculo Volume 1 - 8ª Edição - James Stewart- Ed: 8º - Capítulo 4.5 - Ex. 34
Use o roteiro dessa seção para esboçar a curva.
Passo 1
A questão pede para usarmos a roteiro apresentado na seção do livro para fazer um esboço da curva.
Assim, precisaremos encontrar:
O domínio da função, que são os valores que o pode assumir.
As interseções com eixos, que são os valores de quando e de quando .
Limites no infinito, onde faremos:
Intervalos de crescimento e os pontos críticos, onde analisaremos o sinal da derivada da função, fazendo:
Fazer um estuda da concavidade
E qualquer outra consideração que ajude a entender bem o comportamento da função.
Então vem ver tudo isso.
Passo 2
Nosso primeiro passo é calcular o domínio.
O domínio de uma função é o conjunto de todos os valores de entrada para os quais a função produz um resultado válido.
Sabendo disso, é importante observar as restrições que uma função pode ter.
No caso da nossa função, não existe nenhuma restrição que torna ela inválida.
Dessa forma, o nosso domínio são todos os números reais, ou seja:
Passo 3
Agora precisamos achar os pontos de interceptação nos eixos.
Fazendo , temos o ponto de interceptação no eixo :
Para encontrarmos o ponto de interceptação em fica um pouco complicado, apenas utilizando métodos numéricos.
Assim, o ponto que encontramos já nos dá uma boa base de entendimento.
Passo 4
Vamos verificar se há simetria fazendo :
Logo, percebemos que essa função envolve tanto uma função par como uma função ímpar (somadas), ela não é par nem ímpar.
Além disso, devido a presença do polinômio na função, ela não é periódica.
Passo 5
Como o cosseno é limitado entre e , no infinito, o termo que vai dominar é .
Assim, para , a curva vai se aproximar da reta que é a assíntota oblíqua da função.
Dessa forma, não há necessidades de verificarmos se há assíntotas horizontais e verticais, pois a assíntota horizontal dessa função já exclui a possibilidade de haver outras assíntotas.
Passo 6
Vamos estudar agora o crescimento e decrescimento da curva fazendo a derivada da função.
Derivando a função , temos:
Como (exceto quando ), então a função é crescente.
Passo 7
Para a concavidade usaremos a segunda derivada:
Assim, o sinal do cosseno determinará a concavidade da curva: onde o cosseno for positivo, a concavidade será para baixo (negativa), e onde o cosseno for negativo, a concavidade será para cima.
No nosso caso, o cosseno é negativo, o que justifica a concavidade voltada para cima.
Assim, com base nessas informações, temos a nossa curva:
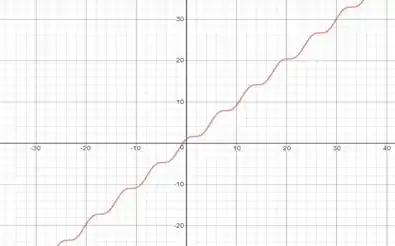
Observe que a função fica oscilando em torno da reta .
Entendeu direitinho?? Responde aeee
Resposta
