Enunciado
Cálculo - Anton - Cálculo - Vol 1- Ed: 10º - Capítulo 1.1 - Ex. 10
Para a função cujo gráfico está na figura abaixo, encontre
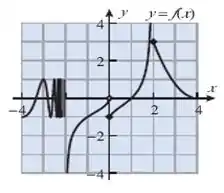
(a)
(b)
(c)
(d)
(e)
(f) as assíntotas verticais do gráfico de .
Passo 1
Aqui a questão pede pra gente dar avaliar o valor da função quando se aproxima (tende) ao valor indicado no limite. Como não temos a função, vamos olhar pelo gráfico.
Vale lembrar que, para um limite existir – ou seja, ter como resposta um número – os limites laterais precisam existir (ou seja, loga acima e logo abaixo do valor de x), e também valer exatamente o mesmo valor do limite desse . Se esses limites laterais não existirem ou forem diferentes, o limite para tendendo a esse ponto não vai existir!
Só pra ficar mais claro, se o limite de x é igual a 1, o limiter de x (ou qualquer outro valor muito muito pequeno) tem que ser aproximadamente 1.
Os limites não vão existir quando forem infinito, seja positivo, ou negativo: .
Sabendo disso, apenas olhando o gráfico – considerando que cada tracinho conta como uma unidade – conseguimos responder as alternativas. Bora lá!
Passo 2
Nesse caso como chegamos em pela esquerda, a função oscila muito! Isso significa que esse limite não existe
Passo 3
Nesse caso conforme vamos chegando em pela direita a função vai pra 3
Passo 4
Nesse caso conforme chegamos pela esquerda a função chega bem pertinho de , apesar do valor da função em ser diferente disso ;)
Passo 5
Indo para pela direita, a função vai pra , que é o valor dessa função em .
Passo 6
Seguindo para pela esquerda, a função sobe muito, isso significa que a função vai pra infinito
Passo 3
g) As assíntotas verticais do gráfico de são as equações das retas em que a função tende ao infinito, seja ou . São as retas e .
Resposta
(a)
(b)
(c)
(d)
(e)
(f) e .