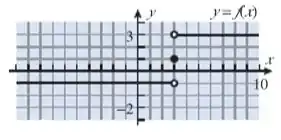
Para a função cujo gráfico está na figura abaixo, encontre

(a)

(b)

(c)

(d)

Aqui, apenas precisamos avaliar o valor da função quando a abscissa se aproxima (tende) ao valor indicado no limite.

Vale lembrar que, para um limite existir – ou seja, ter como resposta um número – os limites laterais precisam existir, e também valer exatamente o mesmo valor do limite na abscissa escolhida. Sendo inexistentes, ou tendo valores diferentes, o limite para tendendo a esse ponto (limite não lateral) não vai existir!

Os limites não existirão quando tiverem como resultado o infinito, seja positivo, ou negativo: . Isso é típico de ocorrer em funções que possuem descontinuidades!

Apenas observando o gráfico – considerando que cada tracinho conta como uma unidade – conseguimos responder as alternativas muito facilmente: