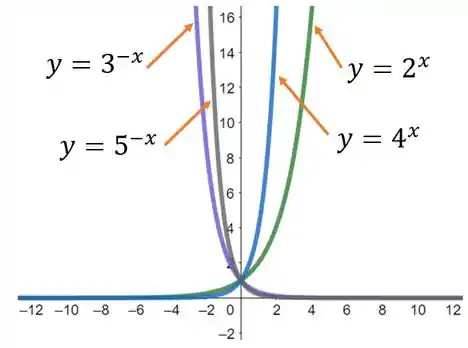
Esboce juntas as curvas dadas no sistema de coordenadas e identifique cada uma com sua equação:
Passo 1
Esta é uma questão que necessita que dois procedimentos sejam realizados: primeiro, o esboço das curvas. Em seguida, que estas curvas sejam identificadas. Fica claro que, ao plotar cada uma das funções, vocês saberão qual função corresponde a qual curva. Entretanto, aqui isto não será deixado claro inicialmente.
Por motivos didáticos, as curvas serão obtidas através de softwares. Após isto, elas serão relacionadas as suas funções a partir das suas características, como se é uma função de crescimento ou decaimento, por exemplo. Vamos então fazer uma breve revisão sobre as funções exponenciais. Estas funções possuem a seguinte forma:
Se o valor de for positivo, esta é uma função de crescimento. Já se for negativo, será uma função de decaimento exponencial. Agora, no caso de uma função exponencial de crescimento, quanto maior for o valor de , mais rápido ela crescerá, e desta forma, é representado graficamente pela maior proximidade com o eixo Y. Já no caso de uma função de decaimento, quanto maior for o valor de , mais rápido será o decaimento. Este fato é representado pela maior proximidade da curva com o eixo Y
Passo 2
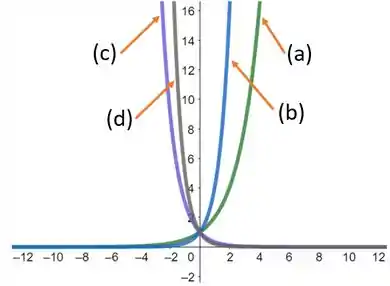
Vamos obter inicialmente o esboço das quatro curvas.
Passo 3
Agora, vamos identificar cada uma das curvas. As curvas de crescimento exponencial são representadas pelas curvas e . Já as de decaimento pelas curvas e . Vamos começar pelas curvas de crescimento.
As funções de crescimento são e , pois o valor de do expoente é positivo . A curva possui um crescimento mais rápido, pois está mais próximo. Portanto, ela é dada pela função . Já a curva , pela função .
Já as funções de decaimento são e , pois o valor de do expoente é negativo . A curva possui um decaimento mais rápido, pois está mais próximo do eixo Y. Portanto, ela é dada pela função . Já a curva , pela função .
Resposta