Enunciado
Cálculo - Cálculo Volume 1 - 8ª Edição - James Stewart- Ed: 8º - Capítulo 6.1 - Ex. 12
Esboce a região delimitada pelas curvas dadas. Decida quando integrar em relação a ou a . Desenhe um retângulo aproximante típico e coloque sua altura e largura. Então, calcule a área da região.
Passo 1
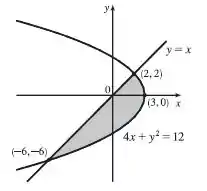
Bom galera, nesse exercício iremos calcular a área da seguinte região delimitada pelas curvas:
Primeiramente, devemos encontrar a interseção das curvas:
Como , temos:
Dessa forma, ou ou e ou . Podemos esboçar a curva. Vamos ter uma reta e uma parábola com concavidade pra esquerda:
Passo 2
Fica mais fácil calcular a integral em relação a , vamos ter as curvas:
ue é a curva a direita, e:
Que é a curva a esquerda e aqui temos o desenho do retângulo aproximante típico:
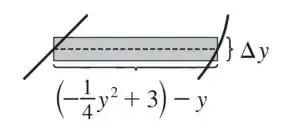
Passo 3
Agora vamos integrar:
A função que vamos integrar é a largura do triângulo aproximante. Nesse caso é mais conveniente integrar em relação a .
Prontinho!