Enunciado
Cálculo - Cálculo Volume 1 - 7ª Edição - James Stewart- Ed: 7º - Capítulo 5.2 - Ex. 40
Calcule a integral, interpretando-a em termos das áreas.
Passo 1
Eaee, belezinha??? Bom... queremos calcular a seguinte integral:
Mas o enunciado pede para interpretarmos em termos das áreas.
Para isso, devemos entender que a integral de uma função é a área sob a curva dessa e que esta é dada por:
Onde é o intervalo de integração!!
Agora bora lá!! 😉
Passo 2
Vamos lá, a integral pode ser interpretada como a área sob o gráfico de entre e , que são os limites de integração do gráfico.
Aqui, como temos um módulo, vamos dividir em duas funções para entender a figura:
Vamos então ter a figura abaixo:
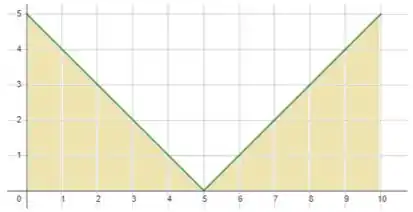
Pela figura vemos que é a área de dois triângulos, ambos com base igual a e altura igual a .
Assim, a integral é a soma dessas áreas:
Entendeu direitinho?? Responde aee 😉