Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Cálculo - Cálculo Volume 1 - 8ª Edição - James Stewart- Ed: 8º - Capítulo 3.9 - Ex. 49

Um velocista corre em uma pista circular de raio 100   m a uma velocidade constante de 7   m / s . Seu amigo está parado a uma distância de 200   m do centro da pista. Quão rápido estará variando a distância entre os amigos quando estiverem a uma distância de 200   m ?

Passo 1

Faaala meu querido.

Nessa questão temos que um corredor numa pista circular de raio dado de 100 m corre a uma velocidade constante de 7 m / s .

Daí, um amigo está parado a uma distância de 200 m do centro da pista.

Queremos saber o quão rápido varia a distância entre os amigos quando eles estiverem a uma distância de 200 m .

Bom, vamos tentar desenhar pra ver se a gente entende melhor.

Vamos alocar esse problema no plano cartesiano de modo que as pessoas são como pontos A = ( x A , y A ) e B = ( x B , y B ) , o centro da pista é a origem e a pessoa B é a que está parada em um ponto qualquer a 200   m do centro da pista.

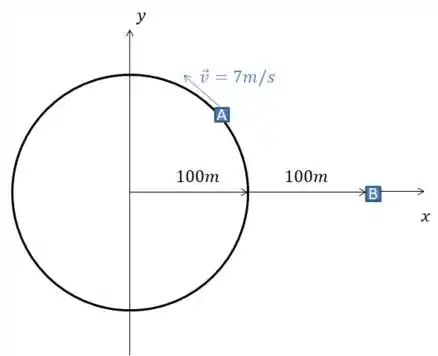
A pessoa A descreve um movimento circular ao redor da origem, com velocidade tangencial v = 7 m s então sua velocidade angular w em função do raio r de circunferência é

v = w r

w = 7 / 100   r a d / s  

Dessa forma, podemos escrever que sua posição é dada por:

x A = r cos ⁡ ( w t ) = 100 cos ⁡ 7 t 100

y A = r sen ⁡ ( w t ) = 100 sen ⁡ 7 t 100

Para a pessoa B , vVamos considerar que está sobre o eixo x a 200   m da origem, logo:

x B = 200

y B = 0

Passo 2

Logo, a distância d entre eles é dada por:

d = x A - x B 2 + y A - y B 2

d = 100 cos ⁡ 7 t 100 - 200 2 + 100 sen ⁡ 7 t 100 2

d = 100 2 cos 2 ⁡ 7 t 100 - 2 × 100 cos ⁡ 7 t 100 × 200 + 200 2 + 100 2 sen 2 ⁡ 7 t 100

d = 100 2 × cos 2 ⁡ 7 t 100 + sen 2 ⁡ 7 t 100 - 40000 cos ⁡ 7 t 100 + 40000

d = 100 2 × 1 - 40000 cos ⁡ 7 t 100 + 40000

d = 50000 - 40000 cos ⁡ 7 t 100

d = 50000 - 40000 cos ⁡ 7 t 100

d = 100 5 - 4 cos ⁡ 7 t 100

d 2 = 100 2 5 - 4 cos ⁡ 7 t 100

Passo 3

Derivando em função de t , temos:

2 d × d ' t = 100 2 4 sen ⁡ 7 t 100 7 100

d ' t = 1400 sen ⁡ 7 t 100 d

Passo 4

Quando a distância d é de 200   m

200 = 100 5 - 4 cos ⁡ 7 t 100

2 = 5 - 4 cos ⁡ 7 t 100

4 = 5 - 4 cos ⁡ 7 t 100

cos ⁡ 7 t 100 = 1 4

Pela lei trigonométrica fundamental:

sen 2 ⁡ 7 t 100 + cos 2 ⁡ 7 t 100 = 1

sen 2 ⁡ 7 t 100 + 1 16 = 1

sen 2 ⁡ 7 t 100 = 15 16

sen ⁡ 7 t 100 = 15 16 = 15 4

Então:

d ' t = 1400 sen ⁡ 7 t 100 d = 1400 15 4 200

d ' t = 7 15 4   ≈ 6,78

Logo, a distância entre os atletas nesse momento varia a uma razão de aproximadamente 6,78 metros por segundo.

Resposta

A distância entre os atletas nesse momento varia a uma razão de aproximadamente 6,78 metros por segundo.

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

A importância no custo total da fabricação de x relógios de uma fábrica é dada por C x = 1500 + 3 x + x 2 c) O custo real da fabricação do quadragésimo primeiro relógio.
Nos Exercícios de 33 a 35, use o conceito de taxa relativa, definido como segue se y = f(x), a taxa relativa da variação de y com relação a x em x1 é dada por f ' x 1 f x 1 ou, equivalentemente, dy /
Mostre que para toda função linear f, a taxa média de variação de f(x) quando x varia de x1 até x1+k é a mesma que a taxa de variação instantânea f(x) em x1.
Nos Exercícios de 33 a 35, use o conceito de taxa relativa, definido como segue se y = f(x), a taxa relativa da variação de y com relação a x em x1 é dada por f ' x 1 f x 1 ou, equivalentemente, dy /
Seja x = f t , t ≥ 0 , tal que f 0 = 1 , d x d t0 e d 2 x d t 20 para t ≥ 0 . Como você acha que deve ser o gráfico de f ? Por quê?