Enunciado
Cálculo - James Stewart - Vol 1- Ed: 8º - Capítulo 6.1 - Ex. 7
Esboce a região delimitada pelas curvas fornecidas. Decida se quer integrar com relação a ou Desenhe um retângulo aproximado típico e identifique sua altura e largura. Então, encontre a área da região.
Passo 1
Primeiramente vamos esboçar a região delimitada pelas curvas plotando-as em um mesmo gráfico. Assim, obteremos
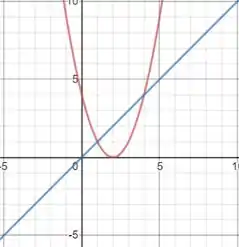
Resta-nos saber onde é que essas curvas vão se interceptar e para isso vamos igualar suas equações fazendo
Resolvendo a equação do segundo grau vamos obter como resultado .
Passo 2
Agora, para encontrarmos a área da região delimitada pelas curvas precisamos calcular a integral da função que está por cima menos a função que está por baixo e os limites de integração serão dados pelos valores de do intercepto das curvas. Então, teremos
Resposta
Exercícios de Livros Relacionados
Nos exercícios de 1 a 29 encontrar a área da região limitada pelas curvas dadas. y = sen xey = - sen x ,x ∈ 0,2 π
Nos exercícios de 1 a 29 encontrar a área da região limitada pelas curvas dadas. y = 2 cosh x 2 , y = 0 ,x = - 2ex = 2
Nos exercícios de 1 a 29 encontrar a área da região limitada pelas curvas dadas. y = 4 - x 2ey = x 2 - 14
Nos exercícios de 1 a 29 encontrar a área da região limitada pelas curvas dadas. y = e x - 1 , y = - xex = 1
Nos exercícios de 1 a 29 encontrar a área da região limitada pelas curvas dadas. y = - 1 - x 2ey = - 2 x - 4