Enunciado
Cálculo - James Stewart - Vol 1- Ed: 8º - Capítulo 6.1 - Ex. 40
Use um gráfico para encontrar as coordenadas aproximadas dos pontos de interseção das curvas dadas. Então indique (aproximadamente) a área da região delimitada pelas curvas.
Passo 1
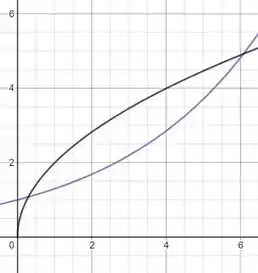
Plotando os gráficos das funções vamos ter o seguinte esboço
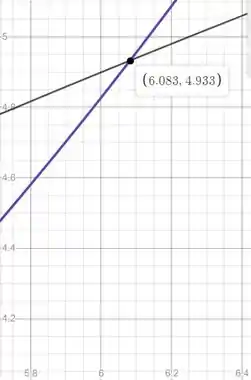
Dando um zoom próximo aos pontos de intersecção dos gráficos vamos encontrar
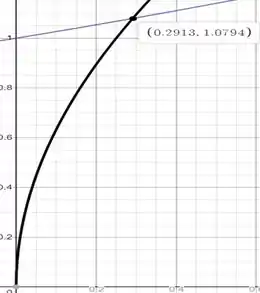
E para o outro ponto teremos
Resposta
Exercícios de Livros Relacionados
Nos exercícios de 1 a 29 encontrar a área da região limitada pelas curvas dadas. y = tg xex = 0ey = 1
Nos exercícios de 1 a 29 encontrar a área da região limitada pelas curvas dadas. x = y 2ey = - x 2
Nos exercícios de 1 a 29 encontrar a área da região limitada pelas curvas dadas. y = cosh xey = senh x ,x = - 1ex = 1
Nos exercícios de 1 a 29 encontrar a área da região limitada pelas curvas dadas. y = cos x ,y = - 3 5 π x + 3 10 ,x ∈ π 2 , 4 π 3
Nos exercícios de 1 a 29 encontrar a área da região limitada pelas curvas dadas. x = y 2 + 1ex + y = 7