Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Cálculo - Cálculo Volume 1 - 8ª Edição - James Stewart- Ed: 8º - Capítulo 6.1 - Ex. 9

Esboce a região delimitada pelas curvas indicadas. Decida quando integrar em relação a x ou y. Desenhe um retângulo aproximante típico e identifique sua altura e largura. Então, calcule a área da região.

y = 1 x ,     y = 1 x 2 ,             x = 2

Passo 1

Bom galera, nessa questão devemos esboçar a região delimitada pelas curvas:

y = 1 x ,     y = 1 x 2 ,             x = 2

Pra começar, vamos achar os pontos de intersecção pra facilitar o desenho:

1 x = 1 x 2 → x = 1

Além disso y = 1 x   e     y = 1 x 2 tocam a reta x = 2 . Assim:

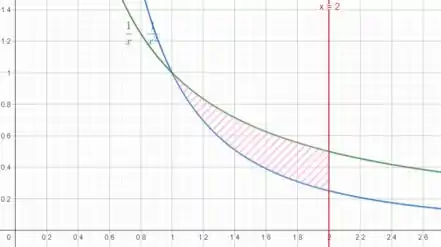
A área entre as curvas é essa rachurada!

Passo 2

Agora só precisamos desenhar o retângulo aproximante. A altura do intervalo será a diferença das funções, ok?

Então:

1 x - 1 x 2

E a largura a variação do x. Vamos desenhar isto!

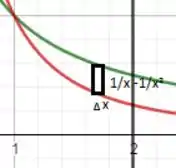
Passo 3

Agora precisamos calcular a área sobre as curvas. Pelo passo anterior temos que:

∫ 1 x - 1 x 2   d x

Uma vez que a função é a diferença de alturas e a largura é Δ x = d x . Os limites de integração são as intesecções que calculamos lá no passo 1:

∫ 1 2 1 x - 1 x 2   d x

Passo 4

Vamos integrar:

∫ 1 2 1 x - 1 x 2   d x = ∫ 1 2 x - 1 - x - 2   d x

∫ 1 2 x - 1 - x - 2   d x = ln ⁡ x - x - 1 - 1 1 2

Aplicando os limites de integração:

ln ⁡ x - x - 1 - 1 1 2 = ln ⁡ 2 - 2 - 1 - 1 - ln ⁡ 1 - 1 - 1 - 1 = ln ⁡ 2 + 1 2 - 1

A = ln ⁡ 2 - 1 2

Prontinho!

Resposta

A = ln ⁡ 2 - 1 2

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

A parábola y = 1 2 x 2 divide o disco x 2 + y 2 ≤ 8 em duas partes. Encontre as áreas de ambas as partes
Encontre a área da região em forma de lua crescente delimitada pelos arcos de raios r e R .
Esboce a região delimitada pelas curvas dadas. Decida quando integrar em relação a x ou a y . Desenhe um retângulo aproximadamente típico e coloque sua altura e largura. Então, calcule a área da regiã