Enunciado
Cálculo - Cálculo Volume 1 - 8ª Edição - James Stewart- Ed: 8º - Capítulo 4.9 - Ex. 51
O gráfico de uma função está mostrado. Qual gráfico é uma primitiva de e por quê?
Passo 1
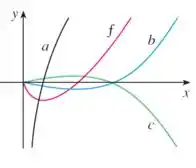
Bom galera, nesse exercício queremos encontrar o gráfico da antiderivada da função no gráfico apresentado:
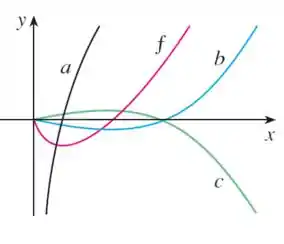
Para isso, iremos utilizar os conceitos de derivada conhecidos! Lembrando que a derivada da primitiva é igual a , então temos que escolher uma função de modo que se comporte como sua derivada!
Passo 2
A primeira coisa que vamos fazer é observar :
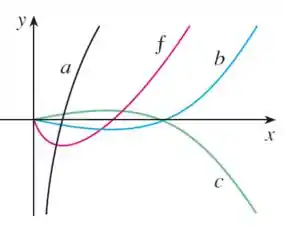
começa em zero e segue com valores negativos, depois ela começa a crescer e toca o eixo . Após isso segue crescendo pra valores de maiores.
Lembrando que:
Se então a sua primitiva é decrescente, pra a primitiva é crescente e em temos um ponto crítico.
Então temos que procurar um gráfico que inicialmente decresce, depois passa por um ponto de mínimo e começa a crescer. Analisando a figura podemos excluir a curva . Pois ela sempre cresce. A curva tem exatamente o comportamento que esperamos!
Já curva cresce, passa por um ponto de máximo e depois decresce, não teria como ser ela também!
Dessa forma a única curva que pode ser primitiva de é a curva .
Resposta
Curva b.