Enunciado
Cálculo - Cálculo Volume 2 - 7ª Edição - James Stewart- Ed: 7º - Capítulo 12.6 - Ex. 42
Esboce a região delimitada pelos paraboloides e .
Passo 1
E aê, galera! Primeiro, bora conhecer melhor esses paraboloides? Olha essa equação:
Como o sinal de ambos os termos quadráticos é positivo, temos que ela representa um paraboloide elíptico com abertura (ou concavidade dos cortes de parábola) voltada para o sentido positivo do eixo . Além disso, o vértice fica na origem, pois o termo constante é zero.
Passo 2
Show! Agora, olha a outra equação:
Nesse caso, como o sinal de ambos os termos quadráticos é negativo, temos que ela também representa um paraboloide elíptico, mas com abertura voltada para o sentido negativo do eixo . Além do mais, o vértice foi deslocado duas unidades para cima do eixo , pois o termo constante é .
Passo 3
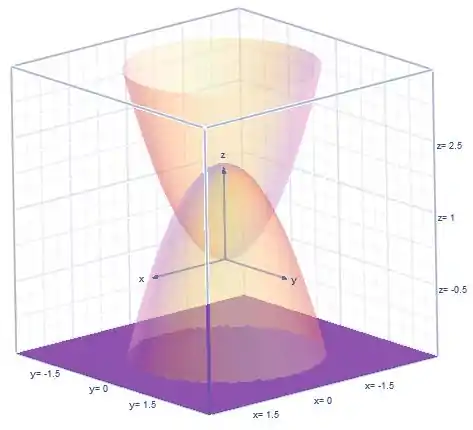
Com as informações acima, se fizermos os esboços dos dois paraboloides, vamos ver que a região delimitada pelos dois está no meio da figura:
Resposta
Ei, a resposta está no passo a passo :)