Enunciado
Cálculo - Cálculo Volume 2 - 8ª Edição - James Stewart- Ed: 8º - Capítulo 10.3 - Ex. 12
Esboce a região no plano que consiste em pontos cujas coordenadas polares satisfazem as condições dadas.
12.
Passo 1
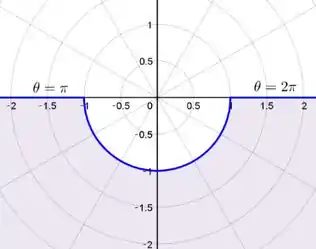
Nessa questão, nós queremos desenhar uma região que obedeça as seguintes condições: . . Explicando com outras palavras: queremos desenhar uma figura com raio maior que , e com abertura angular entre e 2.
Bom, para imaginar isso você pode pensar primeiro em uma circunferência completa, com centro na origem e de raio , se queremos uma região com , essa será para fora dessa circunferência, mas também incluirá a borda dela, pois o raio é maior ou igual a .
Agora para completar o desenho basta olharmos onde ficam as aberturas iguais a e nossa região está situada entre esses dois ângulos.
Fazendo isso, ficamos com o seguinte desenho:
Resposta
Ei, a resposta está no passo a passo :)