Enunciado
Cálculo - Cálculo Volume 2 - 8ª Edição - James Stewart- Ed: 8º - Capítulo 10.3 - Ex. 11
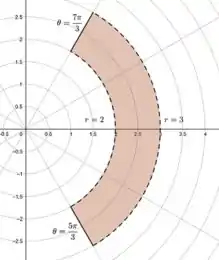
Esboce a região no plano que consiste em pontos cujas coordenadas polares satisfazem as condições dadas.
11.
Passo 1
Nessa questão, nós queremos desenhar uma região que obedeça às seguintes condições:
Explicando com outras palavras: queremos desenhar uma figura com raio maior que dois e menor que três, e com abertura angular entre
Bom, para imaginar isso você pode pensar primeiro em duas circunferências completas e com centro na origem: uma de raio e outra de raio .
Passo 2
A figura que queremos está na região entre as duas, então basta marcarmos onde ficam os ângulos e .
Fazendo isso, ficamos com o seguinte desenho:
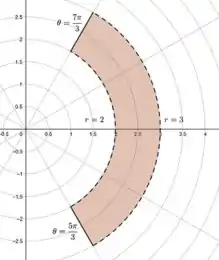
Perceba que o contorno das curvas fica pontilhado pois o raio é estritamente menor que e estritamente maior que , assim, essas bordas não fazem parte da solução.
Resposta
