Enunciado
Cálculo - Cálculo Volume 2 - 8ª Edição - James Stewart- Ed: 8º - Capítulo 10.3 - Ex. 8
Esboce a região no plano que consiste em pontos cujas coordenadas polares satisfazem as condições dadas.
Passo 1
Para esboçar a região no plano cujas coordenadas polares satisfazem as condições e , precisamos entender o sistema de coordenadas polares.
Em coordenadas polares, representa a distância do ponto à origem (raio) e representa o ângulo entre o eixo positivo e a linha que conecta a origem ao ponto (ângulo polar).
Vamos analisar cada condição, preste atenção!!!
1° Condição:
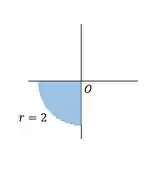
Para significa que a distância do ponto à origem deve ser maior ou igual a zero e menor que 2. Portanto, todos os pontos dentro do círculo com raio 2 (inclusive a borda) satisfazem esta condição.
2° Condição:
Para indica que o ângulo polar deve estar no intervalo de () a (), o que significa que os pontos devem estar localizados abaixo do eixo negativo e acima do eixo negativo.
Passo 2
O gráfico consistirá em um círculo com raio 2, centrado na origem do plano cartesiano. Este círculo representará a primeira condição, , Além disso, para satisfazer a segunda condição, , precisamos considerar os pontos cujos ângulos polares estão no intervalo de a .
Esta região será um quarto de círculo no terceiro quadrante do plano cartesiano, incluindo a parte inferior esquerda do círculo. Todas as coordenadas polares dentro deste quarto de círculo satisfazem as condições dadas.
E então, a região que queremos é:
Resposta
A região no plano é um setor circular de um círculo de raio , limitado pelo ângulo de a e incluindo a borda do círculo.