Enunciado
Cálculo - Cálculo Volume 2 - 8ª Edição - James Stewart- Ed: 8º - Capítulo 10.3 - Ex. 9
Esboce a região no plano que consiste em pontos cujas coordenadas polares satisfazem as condições dadas.
Passo 1
Para esboçar a região no plano cujas coordenadas polares satisfazem e , vamos considerar as coordenadas polares e analisar cada condição.
1° Condição:
Para significa que a distância do ponto à origem deve ser maior ou igual a zero. Portanto, incluímos todos os pontos dentro e fora do círculo com centro na origem e raio infinito.
2° Condição:
Para e indica que o ângulo polar deve estar no intervalo e a , ou seja, entre e . Isso forma um setor circular centrado na origem, limitado pelos raios que formam esses ângulos.
Temos de acordo com o enunciado:
Onde equivale a 45° e equivale a 135°.
Passo 2
Vamos entender como será o gráfico?
O gráfico será uma regiçaõ triangular no plano cartesiano, o eixo x representa a direção horizontal e o eixo y a diração vertical do plano cartesiano.
Que tal algumas características do gráfico. Se liga!
A região triangular é definida pelas seguintes características:
- Inclui todos os pontos à direita do eixo , pois
- Limitada pelo eixo (onde ) à esquerda.
- Limitada pela linha 𝑦=𝑥y=x inclinada a 45 graus no primeiro quadrante.
- Limitada pela linha 𝑦=2𝑥y=2x inclinada a 45 graus no primeiro quadrante.
Visualmente, o gráfico será uma área triangular no primeiro quadrante do plano cartesiano.
- A base da região será o eixo , enquanto o lado direito será definido pela linha e o lado esquerdo pela linha
- A região se estende até infinito ao longo do eixo e .
A região triangular é preenchida, indicando que todos os pontos dentro dela satisfazem as condições em que o ângulo será entre a ,
Desta forma a região no plano descrita é:
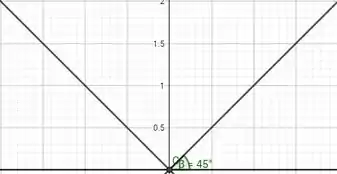
E ai, gostou? Então até a próxima!
Resposta
O gráfico é uma região triangular no primeiro quadrante, limitada pelos eixos e e pela linha , incluindo a origem.