Enunciado
Álgebra Linear e Geometria Analítica - Cálculo Volume 2 - 8ª Edição - James Stewart- Ed: 8º - Capítulo 13.2 - Ex. 4
Escreva cada combinação de vetores como um único vetor.
Passo 1
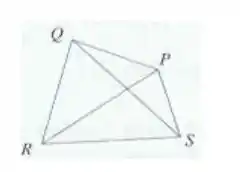
- Usando a regra do triângulo, podemos dizer que
- Usando a regra do triângulo de novo, podemos dizer que
- Olhando nossa figurinha, podemos concluir que
- Usando a regra do triângulo duas vezes, ficamos com:
Passo 2
Passo 3
Passo 4
Resposta
Exercícios de Livros Relacionados
Demonstre que, se V e W são vetores quaisquer de R n , então:a) V ⋅ W = 1 4 [ | | V + W | | 2 ] - | | V - W | | 2 ]( i d e n t i d a d ep o l a r ) ; (Sugestão: desenvolva os segundos membros das igua
Seja { U 1 ,. . ., U n } uma base ortonormal de R n . Se A = [ U 1. . .U n ] é uma matriz n × n cujas colunas são os vetores U 1 ,. . .,U n , então A é invertível e A - 1 = A t . (Sugestão: mostre que
Mostre que se V é ortogonal a W 1 ,. . .,W k , então V é ortogonal a qualquer combinação linear de W 1 ,. . .,W k .
Encontre uma base ortonormal para o plano x + y + z = 0 .
Mostre que o conjunto de todos os vetores do R n ortogonais a um dado vetor V = ( a 1 ,. . ., a n ) , W = { X = ( x 1 ,. . ., x n ) ∈ R n | X ⋅ V = 0 } é um subespaço de R n .