Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Cálculo - Um curso de Cálculo Volume 1 - 5ª Edição - Hamilton Luiz Guidorizzi- Ed: 5º - Capítulo 13.7 - Ex. 7a

Escreva, em coordenadas polares, a equação da elipse x 2 a 2 + y 2 b 2 = 1 , tomando como pólo a origem e como eixo polar o semi-eixo Ox.

Passo 1

Primieramente, vamos fazer o MMC:

b 2 x 2 a 2 b 2 + a 2 y 2 a 2 b 2 =   1

b 2 x 2 +   a 2 y 2 =   a 2 b 2

Primeiramente, sabemos que:

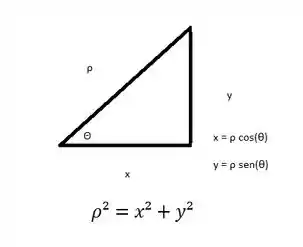
Logo, na primeira parcela:

b 2 ρ ² c o s 2 θ + a 2 ρ ² s e n 2 θ = a 2 b 2

ρ ² = a 2 b 2 b 2 c o s 2 θ + a 2 s e n 2 θ

Resposta

A equação da elipse na forma polar é : ρ ² = a 2 b 2 b 2 c o s 2 θ + a 2 s e n 2 θ

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Nos Exercícios de 5 a 8, uma partícula está sujeita à força horizontal dada e a massa ou aceleração da partícula é dada. Ache a outra quantidade. (8) A força é de 700d i n a s ; a aceleração é de 80c
Nos Exercícios de 5 a 8, uma partícula está sujeita à força horizontal dada e a massa ou aceleração da partícula é dada. Ache a outra quantidade. (7) A força é de 24N ; a aceleração é de 9m / s ² ².
Se f x = ∫ 0 x c o s td t , ache o comprimento do arco do gráfico de f do ponto onde x=0 ao ponto onde x = 1 2 π .
Determine o comprimento das curvas. Se tiver um programa gráfico, talvez queira esboçar o gráfico dessas curvas para ver como elas são x = ∫ 0 y sec 4 ⁡ t - 1 d t - π 4 ≤ y ≤ π 4
Determine o comprimento das curvas. Se tiver um programa gráfico, talvez queira esboçar o gráfico dessas curvas para ver como elas são y = ∫ - 2 x 3 t 4 - 1 d t - 2 ≤ x ≤ - 1