Se , ache o comprimento do arco do gráfico de f do ponto onde x=0 ao ponto onde .
Passo 1
Bom galera, primeiro vamos raciocinar com calma como vamos resolver isso. Primeiro, temos o esboço do gráfico a seguir:
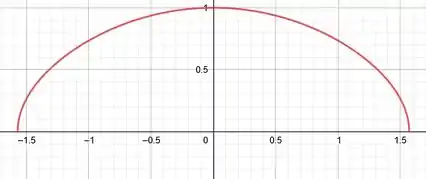
Então queremos achar o comprimento do arco dessa abóboda acima. Para isso, vamos nos utilizar da nossa fórmula:
Passo 2
Temos então que se nosso , nosso
Então calculando o quadrado dessa função, temos que:
Passo 3
Agora, basta substituir o que nos achamos na nossa formula: