a) Escreva, em coordenadas polares, a equação da elipse tomando como pólo a origem e como eixo polar o semi-eixo .

b) Escreva, em coordenadas polares, a equação da elipse tondo como pólo o foco , , e como eixo polar a semireta , onde , . (Faça e .)

No item a), as coordenados polares tem o pólo na origem e o eixo polar no semi-eixo . TODA VEZ QUE ISTO ACONTECER, trata-se do sistema polar PADRÃO, para o qual a transformação entre os sistemas de coordenada é macetada por

É mesmo um macete memorizar as equações acima! Elas são tão uteis que, pra resolver este item, basta substituir elas na equação da elipse, já saindo com a resposta final ô:

Ao contrário do item a), que foi todo macetado pois estávamos no caso “padrão”, o item b) resolve inovar, nos dando um foco e um eixo polar completamente zoados.

Neste caso, a nossa regrinha de substituir e direto não se aplica mais, pois agora as equações para e são diferentes, e devem ser deduzidas!

Mas calma! Se escrevermos o enunciado na forma de um desenho, tudo fica muito mais claro:

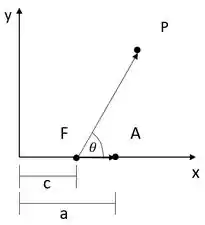
A figura mostra o polo no ponto e eixo polar .

Na figura, desenhamos um ponto arbitrário para deduzir uma relação entre , , e . Agora olha bem, pela figura, qual é a projeção do ponto em e em em função dos valores dados? Dá pra ver que agora temos e também , não dá? Pois bem, acabamos de encontrar a relação que precisamos! Agora basta substituir e na equação da elipse:

Acabou por aqui a questão? Ainda não! O enunciado ainda pede que deixemos o resultado em termos de e .

Vai ser só um trabalhindo de substituição. Na verdade, quando o enunciado pede pra fazermos isso ele no fundo nos fala: “Livre-se e e ! Não quero esses dois aqui!”

Notamos que . Substituindo na nossa equação, temos:

Agora precisamos nos livrar do . Para isso, juntamos as definições de e da seguinte forma:

Ou seja,

Substituindo na equação da elipse e reorganizando um pouco, chegamos na resposta final: