Enunciado
Cálculo - Cálculo Volume 1 - 6ª Edição - James Stewart- Ed: 6º - Capítulo 6.3 - Ex. 21
Escreva, mas não calcule, uma integral para o volume de um sólido obtido pela rotação da região limitada pelas curvas dadas em torno do eixo especificado.
em torno do eixo
Passo 1
Usando o enunciado temos o seguinte esboço:
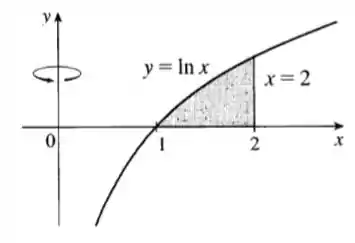
Passo 2
Como podemos ver, a região está limitada em entre e , então nossa integral é:
Isso acontece porque como a função irá girar em torno do eixo , e a distância da função até o eixo é , e ela varia em no intervalo de a , então o raio da circunferência é simplesmente , e sua altura é
Resposta
.
Exercícios de Livros Relacionados
Nos Exercícios 23-26, use o método da casca para determinar o volume dos sólidos obtidos com a rotação das regiões delimitadas pelas curvas dadas em torno das retas dadas.23 - y = 3 x ,y = 0 ,y = 2 A
Nos Exercícios 23-26, use o método da casca para determinar o volume dos sólidos obtidos com a rotação das regiões delimitadas pelas curvas dadas em torno das retas dadas.23 - y = 3 x ,y = 0 ,y = 2 D
Nos Exercícios 23-26, use o método da casca para determinar o volume dos sólidos obtidos com a rotação das regiões delimitadas pelas curvas dadas em torno das retas dadas.23 - y = 3 x ,y = 0 ,y = 2 E
Nos Exercícios 23-26, use o método da casca para determinar o volume dos sólidos obtidos com a rotação das regiões delimitadas pelas curvas dadas em torno das retas dadas.23 - y = 3 x ,y = 0 ,y = 2 E
Nos Exercícios 23-26, use o método da casca para determinar o volume dos sólidos obtidos com a rotação das regiões delimitadas pelas curvas dadas em torno das retas dadas.23 - y = 3 x ,y = 0 ,y = 2 B