Enunciado
Cálculo - Thomas - Vol 2- Ed: 12º - Capítulo 10.2 - Ex. 72
Escreva os primeiros termos das séries para encontrar e e calcule a soma das séries. A seguir, expresse a desigualdade em termos de e encontre os valores de para os quais a desigualdade é válida e a série converge.
Passo 1
Olá galerinha, tudo bem com vocês? Primeiramente vamos relembrar a teoria para séries geométricas! Vem comigo.
As séries geométricas tem a seguinte forma:
Onde e são números reais fixos e . A série pode ainda ser escrita como . A razão pode ser positiva:
com:
- ;
- .
- ;
- .
Ou negativa:
onde:
Se , então quando e . A série converge para:
Lembrando que, a fórmula para a soma de uma série geométrica se aplica quando na expressão (ou o índice , escrevemos a série como ).
Passo 2
Sendo assim, com a seguinte série, conseguimos determinar os valores de e :
Onde:
Com estes valores conseguimos determinar o valor da soma da série:
Passo 3
A série converge quando:
Equações trigonométricas são igualdades que evolvem funções trigonométricas de arcos incógnitos. Para a resolução de equações trigonométricas não existe um processo único, o que devemos fazer é tentar reduzi-las a equações mais simples, do tipo . Iremos considerar que uma solução da equação . As outras possíveis soluções são os arcos côngruos ao arco ou ao arco :
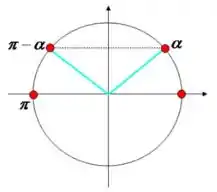
Onde:
- , com ;
- , com .
Com isso, conseguimos concluir que nosso valor de é:
Ou seja:
Sendo assim, temos o seguinte:
e
Onde k é um número inteiro.
Resposta
- ;
- ;
- ;
- ;
.