Enunciado
Cálculo - Cálculo Volume 2 - 5ª Edição - James Stewart- Ed: 5º - Capítulo 15.8 - Ex. 5
Estabeleça a integral tripla de uma função contínua arbitrária em coordenadas cilíndricas ou esféricas sobre o sólido mostrado.
Passo 1
E aí, amigos! Tudo certo?
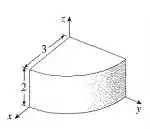
A questão pede para escrevermos uma integral tripla de uma função em coordenadas cilíndricas ou esféricas que descreva a região do sólido da imagem.
O nosso sólido é bem descrito em coordenadas cilíndricas, pois ele descreve um quarto de um cilindro (primeiro octante). Iremos sair de um sistema para um através da seguinte mudança:
Então, o que vamos precisar fazer aqui é escrever nossa integral:
Em coordenadas cilíndricas, expressando tanto nossa função que está sendo integrada quanto nossos limites de integração nesse sistema de coordenadas.
Onde, para as coordenadas cilíndricas:
Vamos juntos!
Passo 2
Vamos começar escrevendo nossa função:
Em coordenadas cilíndricas. Como sabemos:
Então nossa função será:
Passo 3
Já os limites de integração são obtidos diretamente a partir da figura da questão.
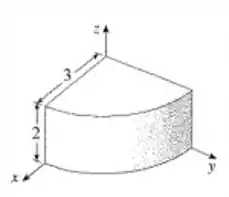
Com ela, sabemos que:
Já que é a altura do sólido.
Já que é o raio do sólido.
Já que o sólido ocupa somente de círculo.
Portanto, a integral tripla que descreve o volume do nosso sólido é: