Enunciado
Cálculo - Cálculo Volume 2 - 8ª Edição - James Stewart- Ed: 8º - Capítulo 15.7 - Ex. 12
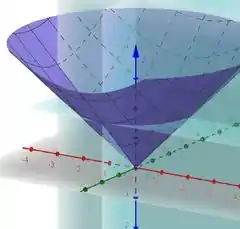
Esboce o sólido descrito pelas inequações.
Passo 1
Fala, pessoal! Tranquilo?
A questão nos dá as inequações:
E:
e pede para que a gente esboçar o sólido que a inequação representa. Para isso podemos manipular nossas equações com outras equações do sistema de coordenadas cilíndricas:
Para e , temos:
Até entendermos qual a forma que está sendo descrita pelas inequações.
Vem!
Passo 2
Nesse exercício iremos analisar as seguintes inequações:
Sabendo que:
Da relação fundamental da trigonometria, temos que , então:
Passo 3
Sendo assim, reescrevendo a equação dada no enunciado, temos:
Como:
Isolando para substituímos na equação :
Substituindo:
Que representa um cone voltado para cima com vértice na origem. O limitante da inequação:
nos diz que o cone só vai até a altura .
Nosso sólido então fica limitado entre:
A restrição
nos diz que o sólido está presente somente no primeiro quadrante, ou seja, é limitado pelos planos e .
Passo 4
O sólido representado pelos limites fornecidos no enunciado é representado a seguir:
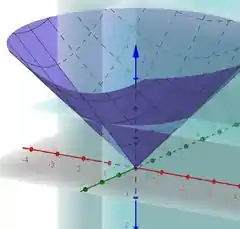
Resposta
